Problem Value: $10$ point$($s$).$ Problem Score: $33\%.$ Attempts Remaining: $9$ attempts.

Help Entering Answers See Proposition $1\mathrm{.}5\mathrm{.}2,$ in Section $1\mathrm{.}5,$ in the MTH $235$ Textbook.

$(10$ points$)$

Homework: Modeling Applications

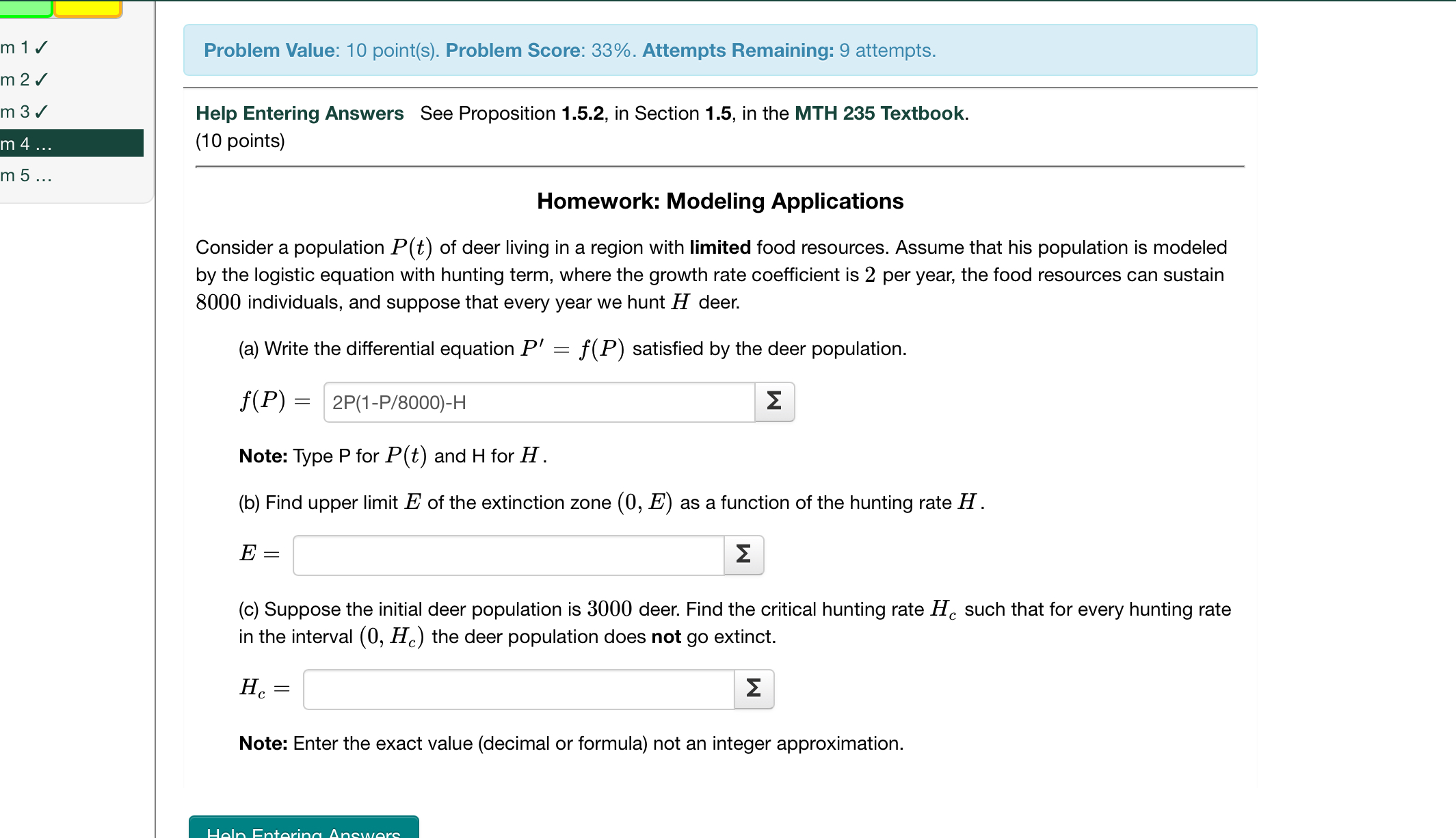
Consider a population $P(t)$ of deer living in a region with limited food resources. Assume that his population is modeled by the logistic equation with hunting term, where the growth rate coefficient is $2$ per year, the food resources can sustain $8000$ individuals, and suppose that every year we hunt $H$ deer.

$($a$)$ Write the differential equation $P^{\text{'}}=f(P)$ satisfied by the deer population.

$f(P)=$

Note: Type P for $P(t)$ and H for $H.$

$($b$)$ Find upper limit $E$ of the extinction zone $(0,E)$ as a function of the hunting rate $H.$

$E=$

$($c$)$ Suppose the initial deer population is $3000$ deer. Find the critical hunting rate $H_c$ such that for every hunting rate in the interval $(0,H_c)$ the deer population does not go extinct.

$H_c=$

Note: Enter the exact value $($decimal or formula$)$ not an integer approximation.