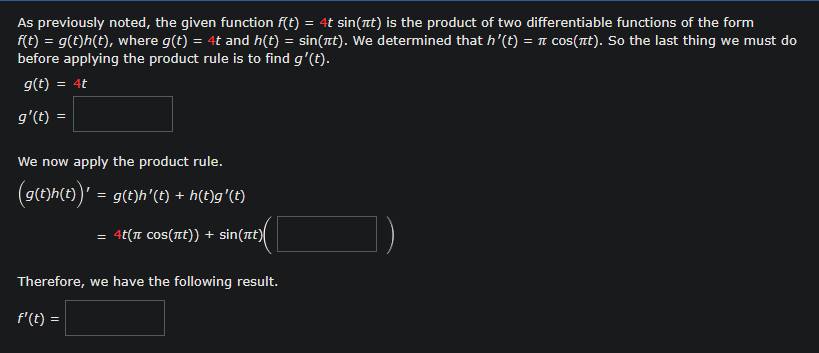
Question: Procedure As previously noted, the given function f(t) = 4t sin(xt) is the product of two differentiable functions of the form f(t) = g(t)h(t), where
Procedure
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


