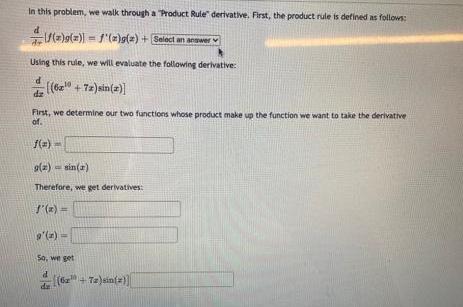
In this problem, we walk through a "Product Rule" derivative. First, the product rule is defined as follows: d f(z)g(z)) = f'(x)g(z) + Select an answer Using this rule, we will evaluate the following derivative: (6x+72) sin(2)] First, we determine our two functions whose product make up the function we want to take the derivative of. f(x)- g(x)=sin(x) Therefore, we get derivatives: J'(x)= 9'(x) = So, we get (62 +72) sin(z