% ******** Program : LiftingLine **********************

% *** Lifting Line Theory ******************

% This program computes the Lift and Ind Drag of a finite wing

% with thin symm. AF sections, no twist

Vinf=50; % Airstream speed

den=1; % air density

b=10; % wing span

N=2; % number of spanwise locations,y,used in the computation

y(1)=0; % y coordinate of wing root

y(2)=b/4; % y coordinate of the middle point; Wing tip is at y = b/2

% Transforming y to theta

for i=1:N

th(i)=acos(-2*y(i)/b);

end

% Assume b,c,zero-lift alpha are known from the airfoil

% section at y.

% enter alpha(angle of attack) and zero-lift alpha

pi=3.1416

a(1)=pi*10/180; % Alpha, 10 degrees for all y's

a(2)=pi*10/180;

a0(1)=0; % Zero-Lift Alpha, for thin, symm. airfoils only !!!!

a0(2)=0;

% enter chord lengths

c(1)=1;

c(2)=0.8;

% Eq. (5.51) applied to diff. spanwise locations

% For N = 2 only !!!(2 spanwise locations)

syms A1 A2

for j=1:N

sum1=A1*sin(th(j))+A2*sin(2*th(j));

sum2=A1*sin(th(j))/sin(th(j))+2*A2*sin(2*th(j))/sin(th(j));

eq(j)=2*b*sum1/(pi*c(j))+a0(j)+sum2-a(j); %For cl slope=2pi only !!

end

% solve for An

[A1,A2]=solve(eq(1),eq(2));

A(1)=eval(A1)

A(2)=eval(A2)

% Local lift ***

for j2=1:N

sum3=0;

for i2=1:N

sum3=sum3+A(i2)*sin(i2*th(j2));

end

G(j2)=2*b*Vinf*sum3 % Local Gamma

L(j2)=den*Vinf*G(j2) % Local lift, Eq. (5.20)

aeff(j2)=a0(j2)+G(j2)/(pi*Vinf*c(j2)) %local alpha-eff

ai(j2)=a(j2)-aeff(j2) % Local induced alpha

Di(j2)=L(j2)*ai(j2) %Local induced Drag

end

% With local lifts at different spanwise locations determined

% ,total lift can be estimated from Eq. (5.25) using,say,the trapezoidal rule

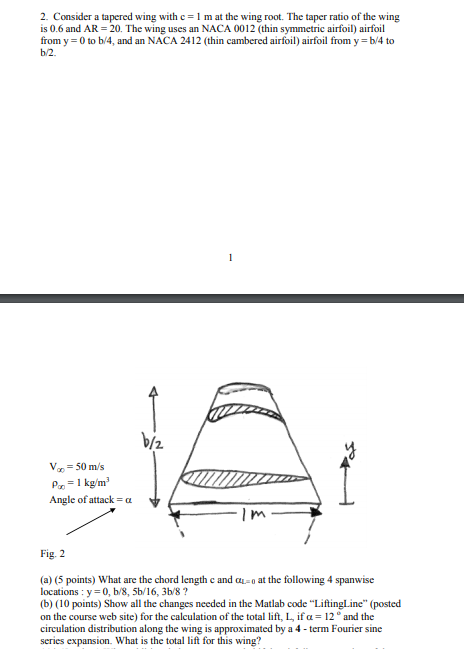
2. Consider a tapered wing with c-1 m at the wing root. The taper ratio of the wing is 0.6 and AR- 20. The wing uses an NACA 0012 (thin symmetric airfoil) airfoil from y - 0 to b/4, and an NACA 2412 (thin cambered airfoil) airfoil from y b/4 to b/2 2. Vo-50m's P1 kg/m Angle ofattack Fig. 2 (a) 5 points) What are the chord length c and a-o at the following 4 spanwise locations : y: 0, b8, 5b/16, 3b8 ? (b) (10 points) Show all the changes needed in the Matlab code "Liftingline" (posted on the course web site) for the calculation of the total lift, L, if ?-12 and the circulation distribution along the wing is approximated by a 4 -term Fourier sine series expansion. What is the total lift for this wing? 2. Consider a tapered wing with c-1 m at the wing root. The taper ratio of the wing is 0.6 and AR- 20. The wing uses an NACA 0012 (thin symmetric airfoil) airfoil from y - 0 to b/4, and an NACA 2412 (thin cambered airfoil) airfoil from y b/4 to b/2 2. Vo-50m's P1 kg/m Angle ofattack Fig. 2 (a) 5 points) What are the chord length c and a-o at the following 4 spanwise locations : y: 0, b8, 5b/16, 3b8 ? (b) (10 points) Show all the changes needed in the Matlab code "Liftingline" (posted on the course web site) for the calculation of the total lift, L, if ?-12 and the circulation distribution along the wing is approximated by a 4 -term Fourier sine series expansion. What is the total lift for this wing