Program the java class listed below ( just the ellipse not the circle)

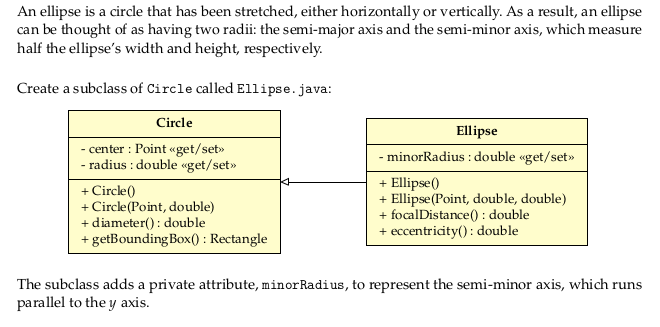
An ellipse is a circle that has been stretched, either horizontally or vertically. As a result, an ellipse can be thought of as having two radii: the semi-major axis and the semi-minor axis, which measure half the ellipse's width and height, respectively. Create a subclass of Circle called Ellipse.java: Circle Ellipse - minorRadius : double get/set>> - center : Point get/set -radius: double get/set >> + Circle + Circle(Point, double) + diameter(): double + getBounding Box(): Rectangle + Ellipse) + Ellipse(Point, double, double) + focalDistance(): double + eccentricity(): double The subclass adds a private attribute, minor Radius, to represent the semi-minor axis, which runs parallel to the y axis. The default constructor should delegate the default Circle constructor, and set the minorRadius equal to the radius this creates the a unit circle. The second constructor takes the center Point, radius, and minorRadius; and uses them to set the parameters of the ellipse. Override width() and height () to the major and minor diameters of the ellipse, respectively. Override diameter() to retum the maximum of the ellipse's width and height. Override area(), perimeter (), and inBounds() according to the following rules: - A = 1.11.12 - P-v2r + r - If the center point of the ellipse is (h,k), then the point (x,y) is inside the ellipse when: (x-h)2 (y - k) > - center : Point get/set -radius: double get/set >> + Circle + Circle(Point, double) + diameter(): double + getBounding Box(): Rectangle + Ellipse) + Ellipse(Point, double, double) + focalDistance(): double + eccentricity(): double The subclass adds a private attribute, minor Radius, to represent the semi-minor axis, which runs parallel to the y axis. The default constructor should delegate the default Circle constructor, and set the minorRadius equal to the radius this creates the a unit circle. The second constructor takes the center Point, radius, and minorRadius; and uses them to set the parameters of the ellipse. Override width() and height () to the major and minor diameters of the ellipse, respectively. Override diameter() to retum the maximum of the ellipse's width and height. Override area(), perimeter (), and inBounds() according to the following rules: - A = 1.11.12 - P-v2r + r - If the center point of the ellipse is (h,k), then the point (x,y) is inside the ellipse when: (x-h)2 (y - k)