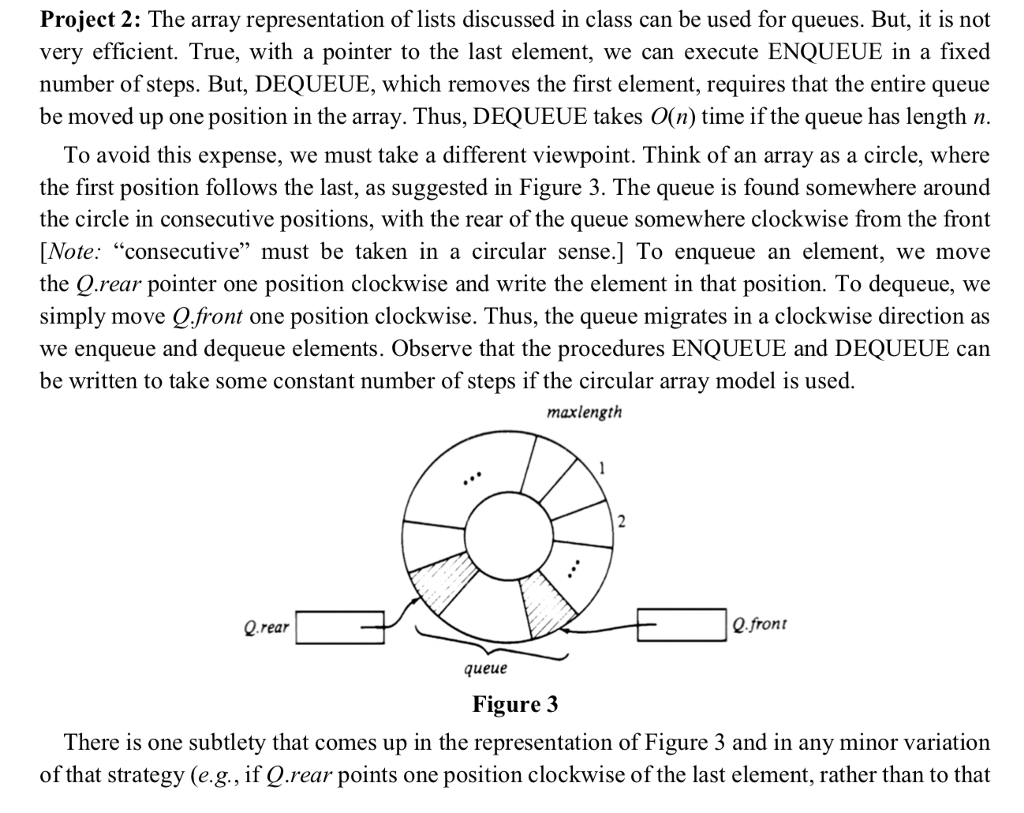
Project 2: The array representation of lists discussed in class can be used for queues. But, it is not very efficient. True, with a pointer to the last element, we can execute ENQUEUE in a fixed number of steps. But, DEQUEUE, which removes the first element, requires that the entire queue be moved up one position in the array. Thus, DEQUEUE takes O(n) time if the queue has length n. To avoid this expense, we must take a different viewpoint. Think of an array as a circle, where the first position follows the last, as suggested in Figure 3. The queue is found somewhere around the circle in consecutive positions, with the rear of the queue somewhere clockwise from the front Note: "consecutive" must be taken in a circular sense.] To enqueue an element, we move the Q.rear pointer one position clockwise and write the element in that position. To dequeue, we simply move Qfront one position clockwise. Thus, the queue migrates in a clockwise direction as we enqueue and dequeue elements. Observe that the procedures ENQUEUE and DEQUEUE can be written to take some constant number of steps if the circular array model is used. maxlength Q rear Q.front queue Figure 3 There is one subtlety that comes up in the representation of Figure 3 and in any minor variation of that strategy (e.g, if Q.rear points one position clockwise of the last element, rather than to that Project 2: The array representation of lists discussed in class can be used for queues. But, it is not very efficient. True, with a pointer to the last element, we can execute ENQUEUE in a fixed number of steps. But, DEQUEUE, which removes the first element, requires that the entire queue be moved up one position in the array. Thus, DEQUEUE takes O(n) time if the queue has length n. To avoid this expense, we must take a different viewpoint. Think of an array as a circle, where the first position follows the last, as suggested in Figure 3. The queue is found somewhere around the circle in consecutive positions, with the rear of the queue somewhere clockwise from the front Note: "consecutive" must be taken in a circular sense.] To enqueue an element, we move the Q.rear pointer one position clockwise and write the element in that position. To dequeue, we simply move Qfront one position clockwise. Thus, the queue migrates in a clockwise direction as we enqueue and dequeue elements. Observe that the procedures ENQUEUE and DEQUEUE can be written to take some constant number of steps if the circular array model is used. maxlength Q rear Q.front queue Figure 3 There is one subtlety that comes up in the representation of Figure 3 and in any minor variation of that strategy (e.g, if Q.rear points one position clockwise of the last element, rather than to that
