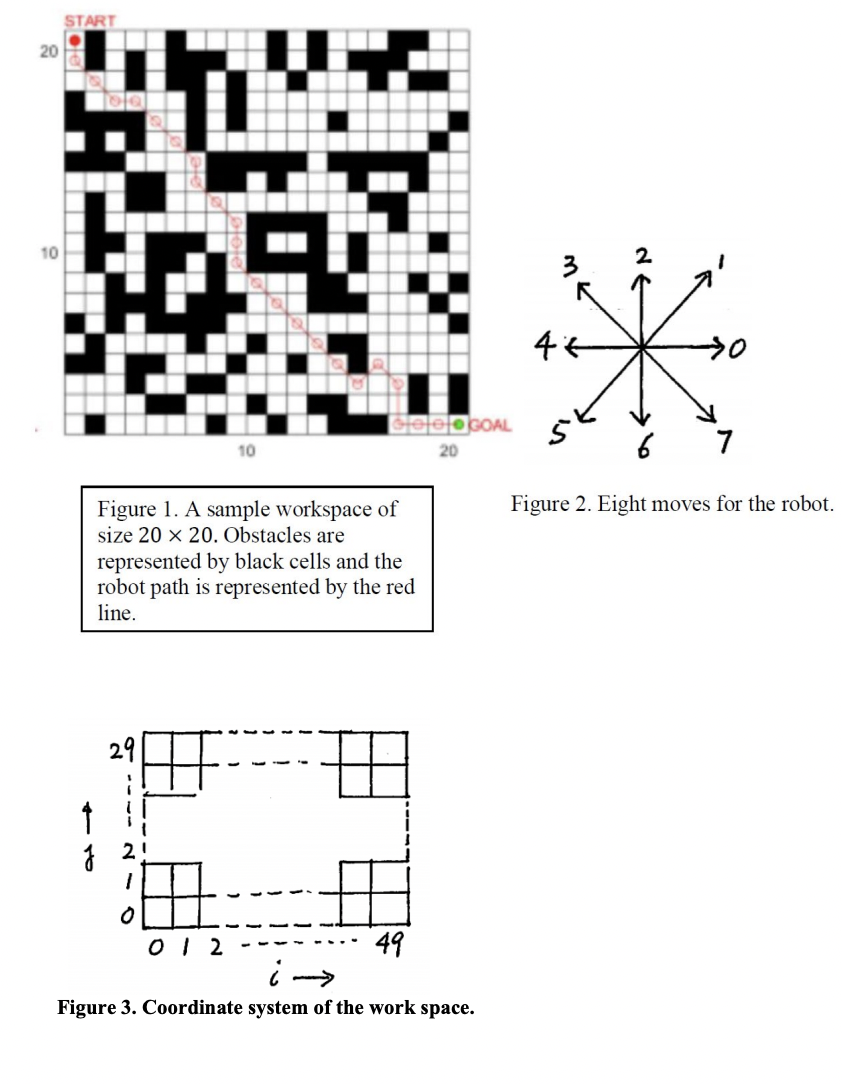
Project Description: Implement the A$*$ search algorithm with graph search $($no repeated states$)$ for the robot path planning problem as described below. The inputs to your program are the start and goal positions of a point robot, and a $2$D integer array that represents the robot workspace. The robot can move from cell to cell in any of the eight directions as shown in Figure $2.$ The goal is to find the lowest$-$cost path between the start position and the goal position, and avoiding obstacles along the path. The workspace is represented as an occupancy grid as shown in Figure $1,$ where the black cells represent obstacles. The red line in the figure depicts a path from the start position to the goal position. $($Note: the path in the figure is not the lowest$-$cost path as required in our project.$)$ Formulation: The problem can be formulated in the following way. Each cell in the workspace is a state. The white cells are legal states and the black cells are illegal states. The actions are the eight moves as defined in Figure $2.$ The step cost for the actions is the sum of the angle cost and the distance cost; i$.$e$.,(,,)=(,,)+(,,)$ where $(,,)=180$ ; let $(,,)=0$ if s is the initial state $($start position$)=|(()()|$; if $>180,$ let $$ equals $360(,,)=1$ for horizontal and vertical moves $0,2,4,6$ and $2$ for diagonal moves $1,3,5,7.$ In the above, s is the current state, a is the action and s$$ is the next state. The angle cost is to penalize any change in the direction of the robot between two consecutive moves. k is a constant that we can set to control the amount of penalty we want to impose for angle change. For the initial state $($start position$),$ we let the angle cost between the initial state s and next state s$$ equals to $0.$ The distance cost is for the distance travelled in an action. Let $()$ be the Euclidian distance between the current position and the goal position. $()$ thus defined is admissible in this problem. During the search, only legal states $($cells without obstacles$)$ will be added to the tree. Input and output formats: The workspace in the test input files is of size $3050($rows x columns.$)$ We will use the coordinate system as shown in Figure $3$ below. The coordinates of the lower$-$left corner cell are $(,)=(0,0).$ The input file contains $31$ lines of integers as shown in Figure $4$ below. Line $1$ contains the $(,)$ coordinates of the start and goal positions of the point robot. Lines $2$ to $31$ contain the cell values of the robot workspace, with $0$s representing white cells, $1$s representing black cells, $2$ representing the start position and $5$ representing the goal position. Line $2$ contains values for $(,)=(,29),$ with $=0$ to $49.$ Line $31$ contains values for $(,)=(,0),$ with $=0$ to $49,$ etc. The integers in each line are separated by blank spaces. Your program will produce an output text file that contains $34$ lines of text as shown in Figure $5$ below. Line $1$ contains the depth level d of the goal node as found by the A$*$ algorithm $($assume that the root node is at level $0.)$ Line $2$ contains the total number of nodes N generated in your tree $($including the root node.$)$ Line $3$ contains the solution $($a sequence of moves from the root node to the goal node$)$ represented by a$$s$.$ The a$$s are separated by blanks. Each a is a move from the set $\{0,1,2,3,4,5,6,7\}.$ Line $4$ contains the f$($n$)$ values of the nodes $($separated by blanks,$)$ from the root node to the goal node, along the solution path. There should be d number of a values in line $3$ and d$+1$ number of f values in line $4.$ Lines $5$ to $34$ contain values for the robot workspace, with $0$s representing white cells, $1$s representing black cells, $2$ representing the start position, $5$ representing the goal position, and $4$s representing cells along the solution path $($excluding the start position and the goal position.$)$ Figure $1.$ A sample workspace of size $\backslash (20\backslash$times $20\backslash ).$ Obstacles are represented by black cells and the robot path is represented by the red line.

Figure $2.$ Eight moves for the robot.

Figure $3.$ Coordinate system of the work space. $```$

nnnn

m m m m m m $....$m

m m m m m m $....$m

$*.$

m m m m m m $....$m

$```$

Figure $4.$ Input file format $(31$ lines.$)$ n$\text{'}$s and $\backslash ($ m $\backslash )\text{'}$s are integers separated by blanks.

$```$

d

N

a a a $....$a

fff$\_....$f

m m m m m m $....$m

m m m m m m$....$m

$...$

m m m m m m $....$m

$```$

Figure $5.$ Output file format $(34$ lines.$)$ d$,$ N$,$ a$\text{'}$s$,$ and m$\text{'}$s are integers. f$\text{'}$s are floating point numbers. The a$\text{'}$s$,$ f$\text{'}$s and m$\text{'}$s are separated by blanks.