proof question :

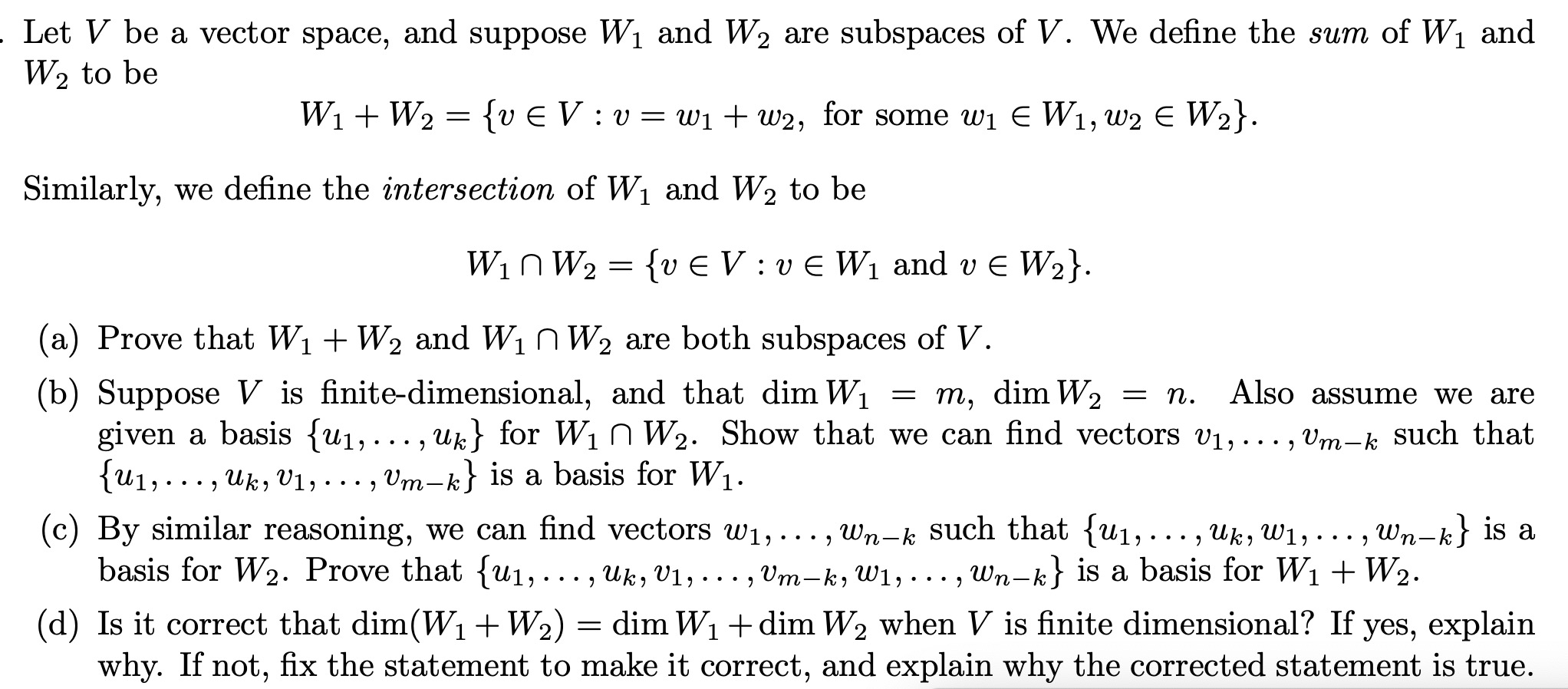
Let V be a vector space, and suppose Wi and W2 are subspaces of V. We define the sum of W, and W2 to be W1+ W2 = {vEV : v= W1 + w2, for some w1 E W1, W2 E W2}. Similarly, we define the intersection of W1 and W2 to be WinW2 = {uEV : vE W1 and v E W2}. (a) Prove that W1 + W2 and Win W2 are both subspaces of V. (b) Suppose V is finite-dimensional, and that dim W1 = m, dim W2 = n. Also assume we are given a basis {ul, ..., uk} for WI n W2. Show that we can find vectors v1, ..., Um-k such that (u1, . .., Uk, VI, . .., Um-k) is a basis for W1. (c) By similar reasoning, we can find vectors w1, ..., Wn-k such that {u1, . .., Uk, W1, ..., Wn-k) is a basis for W2. Prove that {ul, . .., Uk, V1, ..., Um-k, W1, ..., Wn-k} is a basis for W1 + W2. (d) Is it correct that dim(W1 + W2) = dim W1 + dim W2 when V is finite dimensional? If yes, explain why. If not, fix the statement to make it correct, and explain why the corrected statement is true