PROPERTIES: 1. Associativity: 1.1. R + (S + T) = (R + S) + T 1.2. R (S T) = (R S) T 2. Commutativity: R + S = S + R 3. Distributivity: 3.1. R (S + T) = R S + R T 3.2. (S + T) R = S R + T R 4. Identity element: 4.1 R + = + R = R 4.2 R = R = R 5. Neutral element: R = R = 6. Idempotence: 6.1. R+R=R 6.2. (R^{})^{} = R^{} 7. Properties of the Kleene lock: 7.1. ^{}= 7.2. ^{} = 7.3. R^{+} = R R^{} = R^{} R 7.4. R^{} R^{} = R^{} 7.5. R^{} = + R^{+} = R^{+} + 7.6. R? = R + = + R 7.7. (R + S)^{} = (R^{} S^{} )^{} = (R^{} S)^{} R^{} 7.8. (R S)^{} = + R (S R)^{} S 7.10. R (S R)^{} = (R S)^{} R 8. Conditional properties: 8.1. If L(R) L(S), then R + S = S 8.2. If L(R^{}) L(S^{}), then R^{} S^{} = S^{} 8.3. If L(R^{}) L(S^{}), then (R + S)^{} = S^{}

EXERCISE 1. LEGIBLE HANDWRITING 2. I WILL VOTE WITH HAND UP IMMEDIATELY ONLY IF YOUR ANSWER IS CORRECT 3. DRAW THE DIAGRAMS OF THE AUTOMATONS WITH CIRCLES, AS INDICATED IN E)

read to be able to solve it as indicated: a) Thompson's algorithm

b)

nondeterministic finite automaton (AFN)

c)

d)

e)

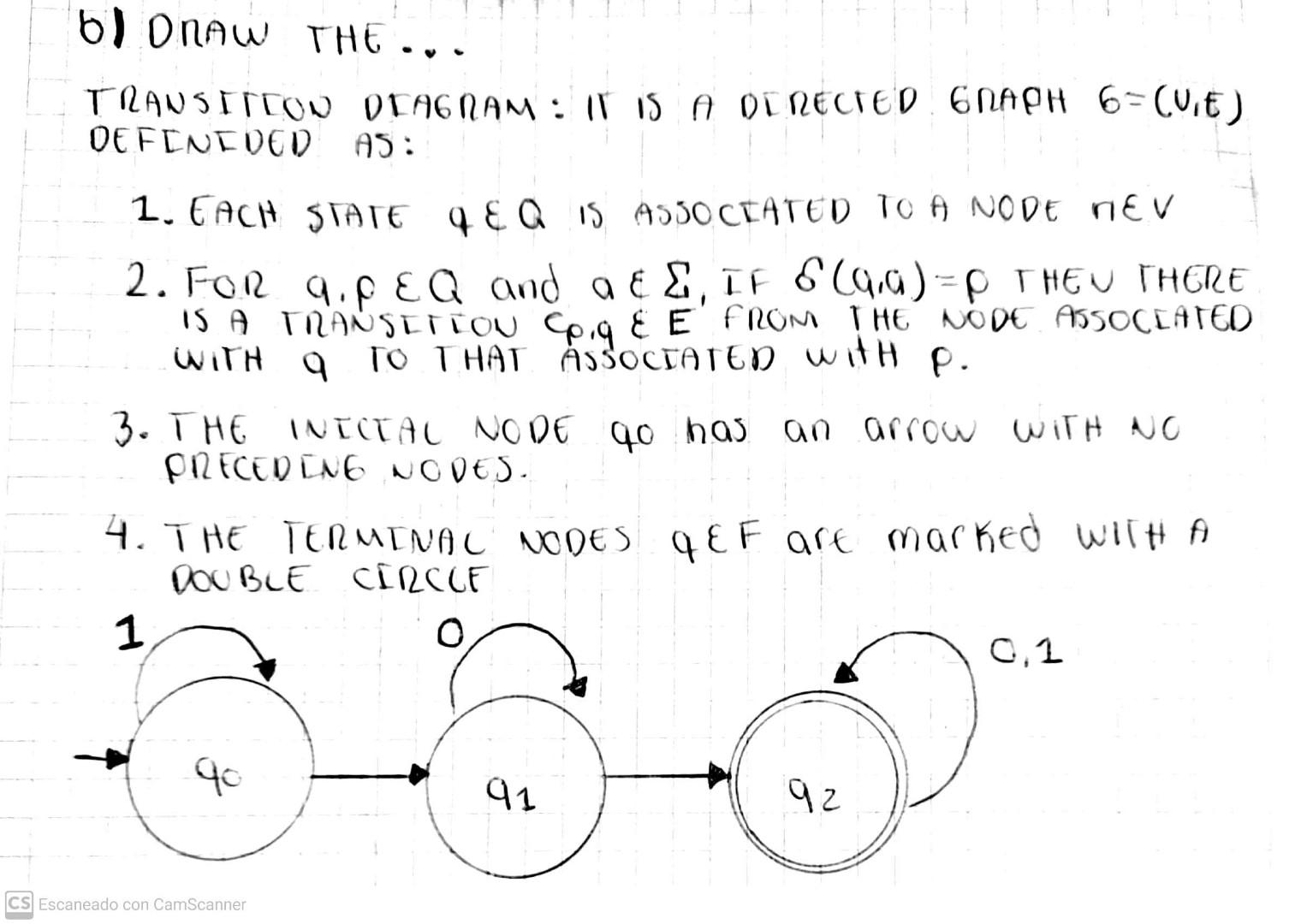
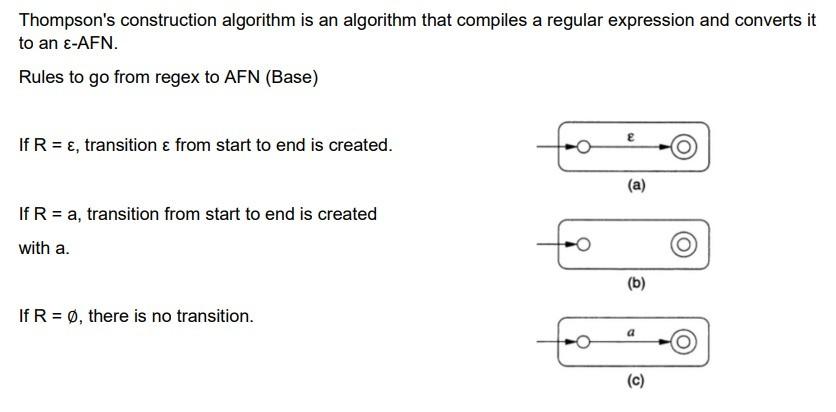
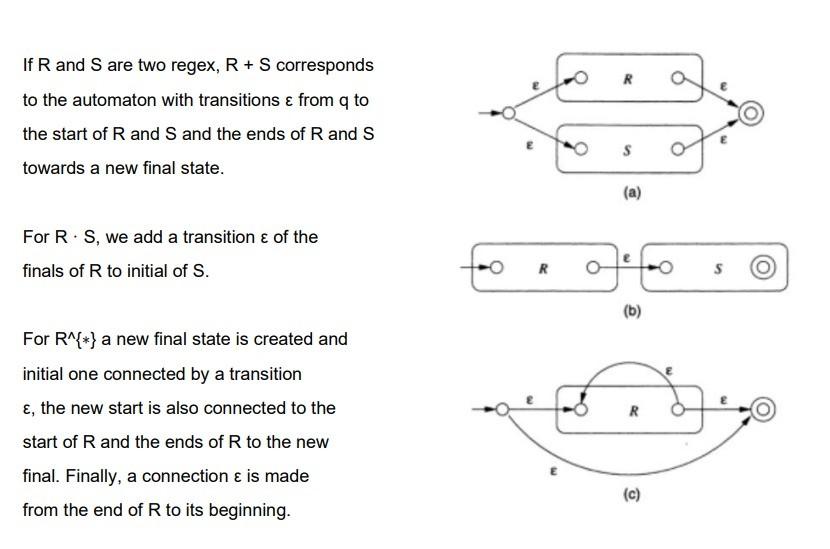
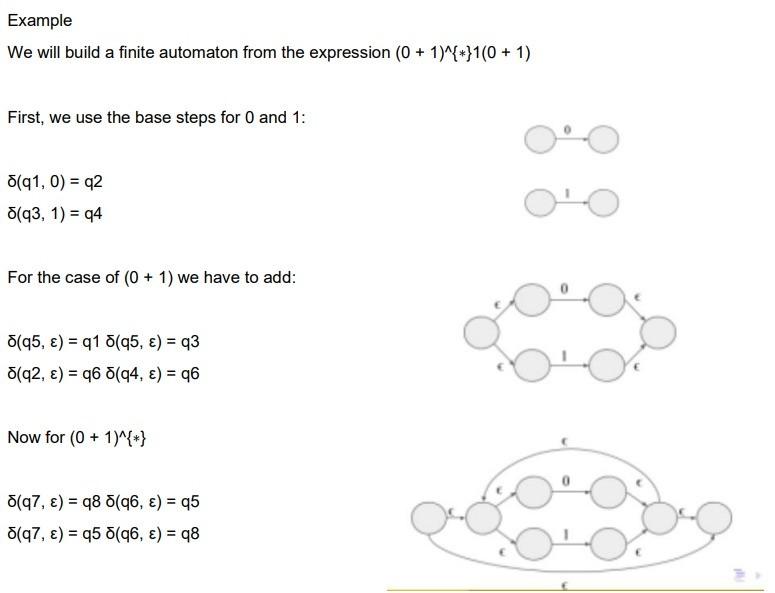
from the followeng regular expression: (0?^+1)1+ a) generate the finete automata using the THOMPSON CONSTRUCTLON ALGORITHM AN ORAW THE DLAGRAM. b) USE THE ALGORLTHM TO TRANSFORM IT INTO AN AFD. DRAW THE DIAGRAM. C) APPCY THE TABLE FIULNG ALGORITHM TO OBTAEN DISTINGUISHABLE STATES AND EQUIUACENT. d) APPLY THE AlGORITHM TO FIND THE MINIMUM AUTOMATA. DRAW THE DIAGRAM. Thompson's construction algorithm is an algorithm that compiles a regular expression and converts it to an AFN. Rules to go from regex to AFN (Base) If R=, transition from start to end is created. If R=a, transition from start to end is created with a. If R=, there is no transition. If R and S are two regex, R+S corresponds to the automaton with transitions from q to the start of R and S and the ends of R and S towards a new final state. For RS, we add a transition of the finals of R to initial of S. For R{} a new final state is created and initial one connected by a transition , the new start is also connected to the start of R and the ends of R to the new final. Finally, a connection is made from the end of R to its beginning. Thompson's construction algorithm (Base) Example We will build a finite automaton from the expression (0+1){}1(0+1) First, we use the base steps for 0 and 1 : 0 (q1,0)=q2(q3,1)=q4 1 For the case of (0+1) we have to add: (q5,)=q1(q5,)=q3(q2,)=q6(q4,)=q6 Now for (0+1){} (q7,)=q8(q6,)=q5(q7,)=q5(q6,)=q8 1: procedure To-AFD (N=(QN,,N,q,FN)) 2: QD=P(QN), the new states are sets of states of the AFN 3:{q} is the initial one. 4:FD={SQ:SFN=} 5: For all SQ and : D(S,a)=pSN(p,a) 6: Unreachable states are discarded. 7: return D={QD,,D,{q},FD} 8: end procedure 1:2:3:4:5:6:7:8:9:0:1:2:procedureMinimize(A=(Q,,,q0,F))TTABLE-FILling(A)QequivEQUivalenT-States(T)Q/PARTITION(Q,Qequiv)q0[q0]F[qf]for[q]Q/,adoif[q]=[p]and(q,a)[p]then([q],a)=[p]endifendforendprocedure TRANSITLON DLAGRAM: II IS A DIRECTED GRAPH 6=(U,E) DEFINIDED AS: 1. EACh sTATE qEQ is asJoctated to a NOdE rEE 2. FOR a,p EQ and a E III(a,a)=P THeU THERE IS A TRANSITIOU CP,q E E' FROM IHE NODE ASSOCLATED WITH 9 TO THAT ASSOCIATED WIHH P. 3. THE INICTAL NODE qO has an arrow WITH NC PRECEDLNG NODES. 4. THE TERMINAL NODES QEF arE marked WIIHA