prove by using the same format and method as the example

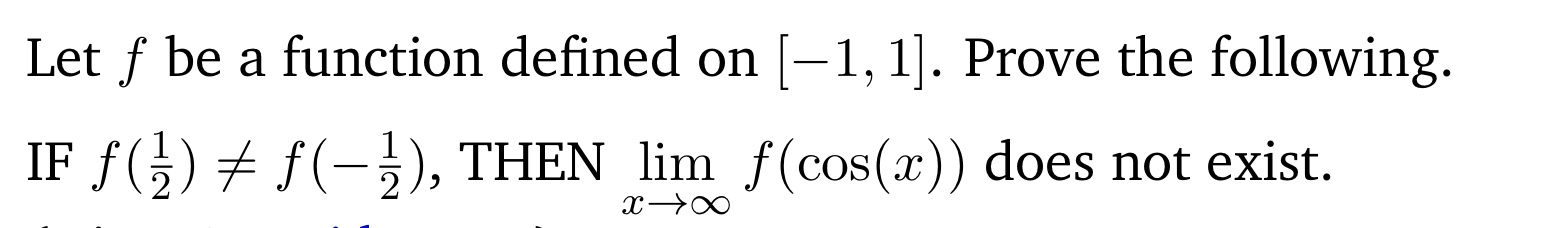
4. Let f be a function with domain (-co, 0) U (0, co). Prove that IF lim f (x) = 00 x-+0 THEN lim f(x) does not exist x-+0 Notes: Before you write this proof, make sure you understand the precise definition of "the limit is co" and the definition of "the limit does not exist". Notice that the definition of "the limit does not exist" is not the negation of "the limit is L". If your definitions are not correct, then your proof cannot possibly be correct, and you won't get any credit. Make sure to write a formal proof directly from the formal definitions, without using any limit laws or similar properties. Remember that: (a) "lim f(x) = 00" means: x-0 ( IN > >0) '>A '0 > >0) 'HE '0 > TA Proof of the statement: We assume that lim f(x) = co and we want to show that lim f(x) doesn't exist. x-0 x-+0 . Let LER. . Take = = 1. Notice that = > 0. (Note: in this problem, any choice of & would work, but we do need to choose one.) . Let S > 0. . Since lim f(x) = oo, (using M = L + 1 in the definition), there exists 61 > 0 such that for every x E R, if 0 L + 1. (1) . Take x = min {?, 2 }. Notice that (x| = x and x * 0. - Then we have that 0 L + 1. Therefore f(x) - L > 1 and thus If (x) - L| > 1 = E. . We have verified that 0 E, as we needed.Let f be a function defined on -1, 1]. Prove the following. IF f() + f(-3), THEN lim f (cos(ac)) does not exist