Prove that for any minimum spanning tree T for a connected, undirected graph G with positive (and not necessarily distinct) edge weights, and for any pair of vertices u,v, and any path P from u to v in G, the maximum weight edge along P has a weight that is at least as high as the maximum weight edge along the unique simple path from u to v in T.

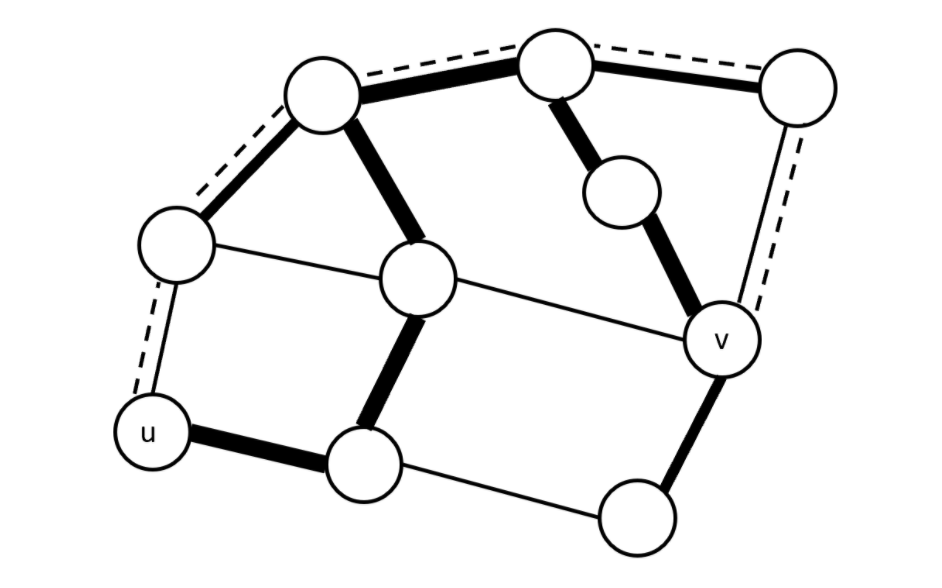
Example: can path P (the dashed edges) have a maximum weight edge lighter than the maximum weight edge along the simple path (boldest edges) from u to v along the MST (bold edges)?

n