Prove that if n is an integer and 3n + 2 is even ,then n is even using a proof by contradiction

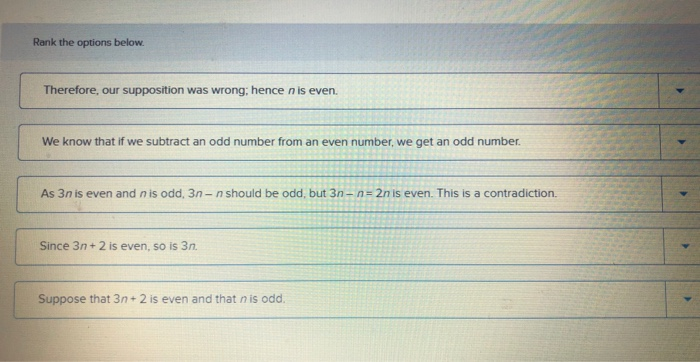
Rank the options below. Therefore, our supposition was wrong; hence n is even We know that if we subtract an odd number from an even number, we get an odd number. As 3n is even and n is odd, 3n-n should be odd, but 3n-n=2n is even. This is a contradiction. Since 3n+2 is even, so is 3n. Suppose that 3n+2 is even and that is odd