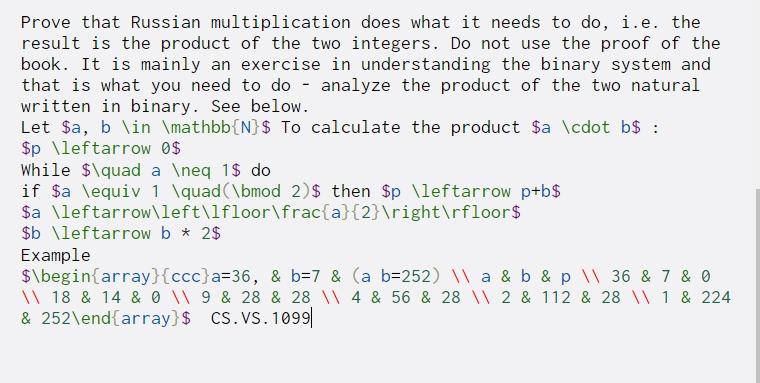
Prove that Russian multiplication does what it needs to do, i.e. the result is the product of the two integers. Do not use the proof of the book. It is mainly an exercise in understanding the binary system and that is what you need to do - analyze the product of the two natural written in binary. See below. Let $a, b \in \mathbb{N} $ To calculate the product $a \cdot b$ : $p \leftarrow 0$ While $\quad a eq 1$ do if $a \equiv 1 \quad(\bmod 2)$ then $p \leftarrow p+b$ $a \leftarrow\left\lfloor\frac{a}{2} ight floor $ $b \leftarrow b * 2$ Example $\begin{array}{ccc}a=36, & b=7 & (a b=252) a & b & p \\ 36 & 7 & 0 18 & 14 & 09 & 28 & 28 \\ 4 & 56 & 28 1 2 & 112 & 28 \\ 1 & 224 & 252\end{array} $ CS.VS. 1099|