Prove that these two equations are equal when N -> infinity (or when N is a very large number):

Equation 1: (hypergeometric distribution)

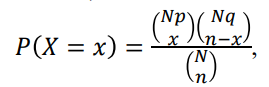
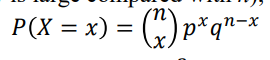
Np Nq n-x P( X = x) N nn P(X = X n-xRelation btw Hypergeometric and Binomial Distribution . Let the total number of blue and red marbles be N, while the proportions of blue and red marbles are p and q=1-p respectively, then: b P = b+r ,q = b+r or b = Np, r = Nq The hypergeometric distribution, its mean and variance will become: (x = X)d (* ) npq (N-n) u = np, 02 = (* * N-1 . Note that as N - co (or N is large compared with n), (*) and (* *) will become: P ( X = x) = (pxqn-x H = np, 02 = npq This indicates that for large N, sampling without replacement is practically identical to sampling with replacement. In other words, hypergeometric distribution is identical with binomial distribution when N is large