Question: prove that this is a tautology using the given steps b) [(-)(-+) -- (0-1) (pv) A(-9vn] (qv) by logical equivalence -10-)^(+ n] v (+by logical
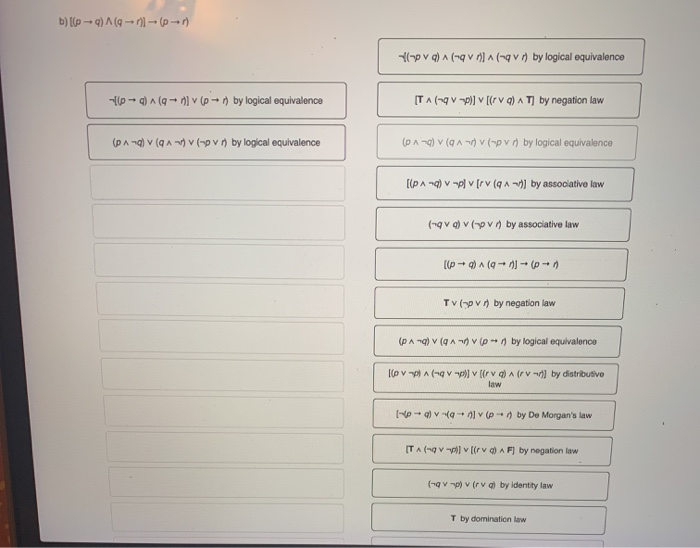
![[(-)(-+) -- (0-1) (pv) A(-9vn] (qv) by logical equivalence -10-)^(+ n] v](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66ef368a7a536_09766ef3689bd26a.jpg)
b) [(-)(-+) -- (0-1) (pv) A(-9vn] (qv) by logical equivalence -10-)^(+ n] v (+by logical equivalence ITA(-9V-p)] [(ra) AT] by negation law (A-) (94-) (-ovo) by logical equivalence (04-) V(A) (pv) by logical equivalence [(PA-) V-p] [rv (94 by associative law (nova) (pv) by associative law [(p+ 4) A (9- ) + (-1) TV (pv) by negation law (Ang) (A v o ) by logical equivalence Iov - (-9V-vira) Arv-] by distributivo law - -- -(+] (+) by De Morgan's law ITA-V-vira) AF) by negation law (-9v-p) virva) by identity law T by domination law T by domination law -[(p+ 9) ^ (9 nl v (pm) by logical equivalence (p^-) v (pvn) v (94-) by commutative law D (op v g) v [(-qvn) v-(-9vn] by logical equivalence
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


