Question: Prove the following problem using mathematical induction. 1*2*3 + 2*3*4 + ... + n(n + 1)(n + 2) = n(n + 1)(n + 2)(n +

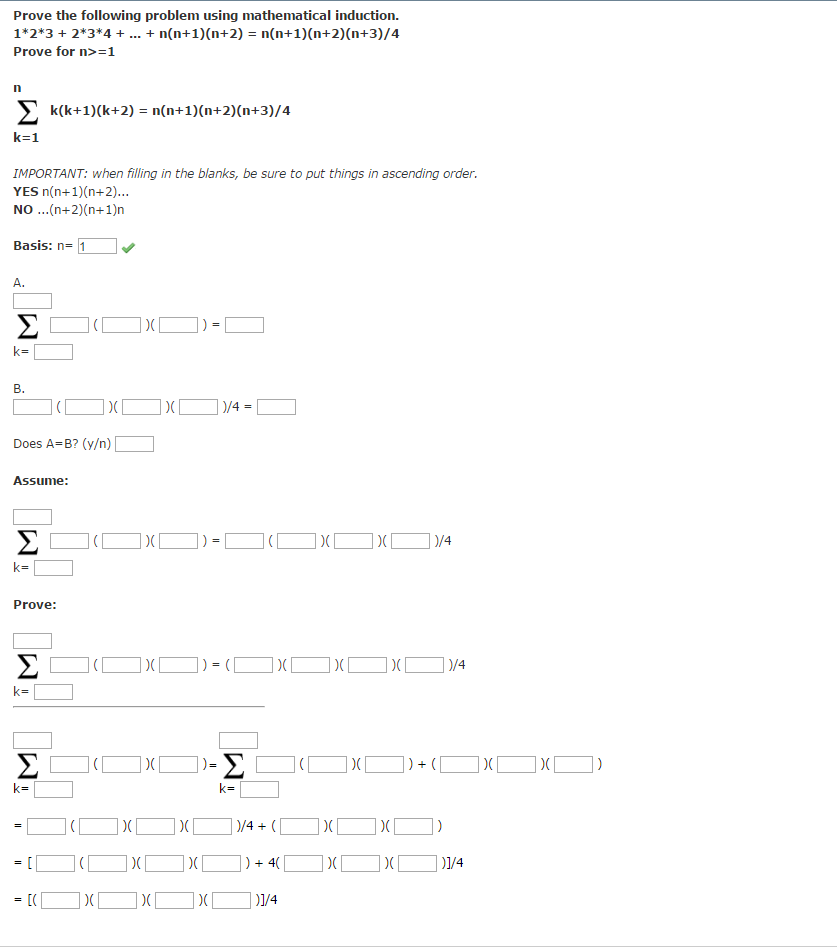
Prove the following problem using mathematical induction. 1*2*3 + 2*3*4 +

Prove the following problem using mathematical induction. 1*2*3 + 2*3*4 + ... + n(n + 1)(n + 2) = n(n + 1)(n + 2)(n + 3)/4Prove for n> = l Sigma_k = 1^n k(k + 1)(k + 2) = n(n + 1)(n + 2)(n + 3)/4 IMPORTANT: when filling in the blanks, be sure to put things in ascending order. YES n(n+1)(n+2)... NO ...(n+2)(n+1)n Basis: n = 1 A. Sigma_k = _____^_____ _____ (_______)(_______) = ___________ B. ______(_______) (_______)(_______)/4 = ________ Does A - B? (y) ________ Assume: Sigma_k = ___^________ _______(_______) (_______) = (_______)(_______)(_______)(_______)/4 Prove: sigma_k = _______^______ _________ (_______)(_______) = (_______)(_______)(_______)/4 sigma_k = _______^______ ___________ (_______)(_______) = sigma_k = ______^_____ ______(_______) (_______) + (_______)(_______)(_______) = __________ (_______)(_______)(_______)/4 + (_______)(_______)(_______) = (_______)(_______)(_______)(_______) + 4(_______)(_______)(_______)/4

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Q:

Prove the following statement using mathematical induction EXAMPLE 1 Prove that, for any positive integer n, 1+ 2+ 3+...+ /= n(n +1) 2 Solution: n 1+ 2 13 +. .. + 10 = 10 (10+1) Step 1: P (1 ) 2 1 =...

Q:

ICS 3 1 1 : Algorithms Spring 2 0 2 4 Problem Set 1 Prof. Nodari Sitchinava Due: Friday, January 1 2 , 2 0 2 3 at 4 pm You may discuss the problems with your classmates, however you must write up the...

Q:

1: Refinancing a loan. Suppose someone takes out a home improvement loan for $30,000. The annual interest on the loan is 6% and is compounded monthly. The monthly payment is $600. Let an denote the...

Q:

EXERCISE 8.4.2: Proving identities by induction. ? Prove each of the following statements using mathematical induction. (a) ;3 n(n + 1) 2 Prove that for any positive integer n, 2 (b) Prove that for...

Q:

I need help with e, f. Exercise 4.12.2: Proving identities by induction. i About n2 Prove each of the following statements using mathematical induction (a) 2 n(n+1) Prove that for any positive...

Q:

Question c EXERCISE 8.5.1: Proving divisibility results by induction. Prove each of the following statements using mathematical induction. (a) Prove that for any positive integer n, 4 evenly divides...

Q:

'8, EXERCISE 8.5.1: Proving divisibility results by induction. Prove each of the following statements using mathematical induction. (a) Prove that for any positive integer n, 4 evenly divides 32n-'l....

Q:

3. If today is Tuesday, what day of the week will it be 900 days from now? 3. (8 points) Consider the Venn diagram shown below. Shade the region corresponding to the set (BUC) - A. (a) Saturday (c)...

Q:

Prove each of the following statements using mathematical induction. For each statement, answer the following questions: a. What is the base case? b. Complete the basis step of the proof by showing...

Q:

Prove each of the following statements using mathematical induction. (b) For any n greaterthanorequalto 1, the factorial function, denoted by n!, is the product of all the positive integers through...

Q:

Let a = 2i - j + k, b = + 3j + 2k, and c = i + 2j - k. Find each of the following: a. a b b. a (b + c) c. a (b c) d. a (b c)

Q:

Use options with strike K2 = $20.00: a. Draw a covered put (long stock plus long put) profit diagram. b. Give a reason why a trader might want to hold a covered put position. c. Explain the...

Q:

The fairest method for calculating interest on an account used _ _ _ _ method for determining the balance to which the interest rate is applied. Question 4 9 Select one: a . minimum - balance b ....

Q:

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

Q:

What qualities do you see as necessary for your line of work?

Q:

Write down a set of values that are important to you. Ask family members and friends to encourage you to live according to your values.

Q:

Describe key areas of your life that are important to you, and write down one or two goals in each major area. Select one or two goals and imagine the goal(s) being achieved to your full...