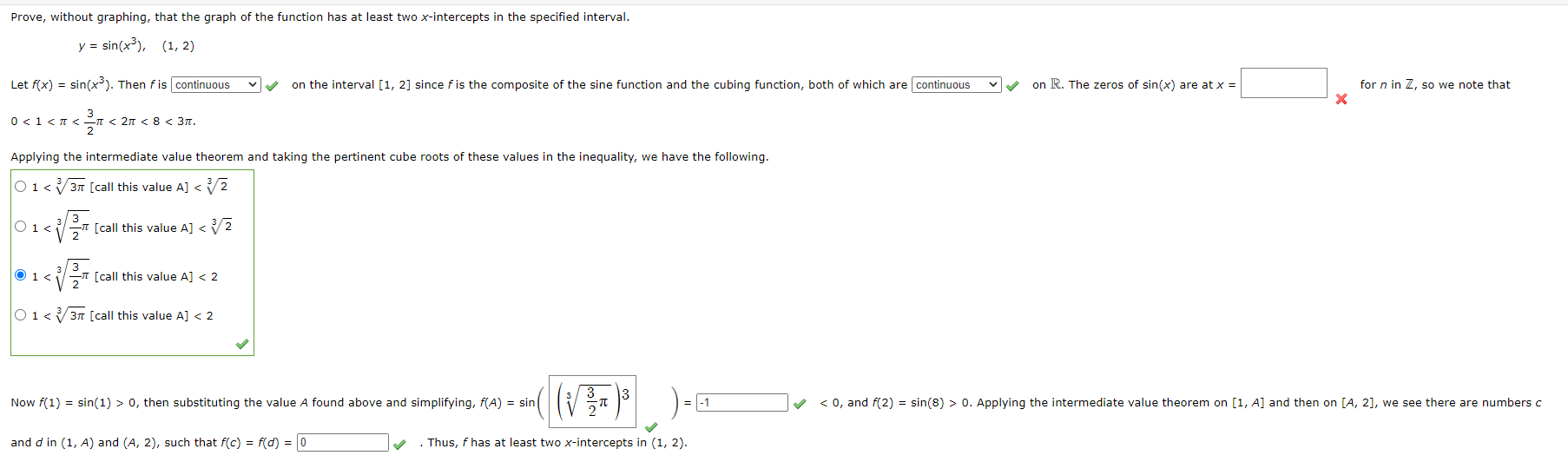
Prove, without graphing, that the graph of the function has at least two x-intercepts in the specified interval. y = sin(x ), (1, 2) Let f(x) = sin(x ). Then fis continuous v v on the interval [1, 2] since f is the composite of the sine function and the cubing function, both of which are | continuous v v on R. The zeros of sin(x) are at x = for n in 2, so we note that X O 0, then substituting the value A found above and simplifying, f(A) = sin R 3 = 1 0. Applying the intermediate value theorem on [1, A] and then on [A, 2], we see there are numbers c and d in (1, A) and (A, 2), such that f(c) = f(d) = 0 . Thus, f has at least two x-intercepts in (1, 2)