Provide a dynamic programming solution to the problem by following the described steps:

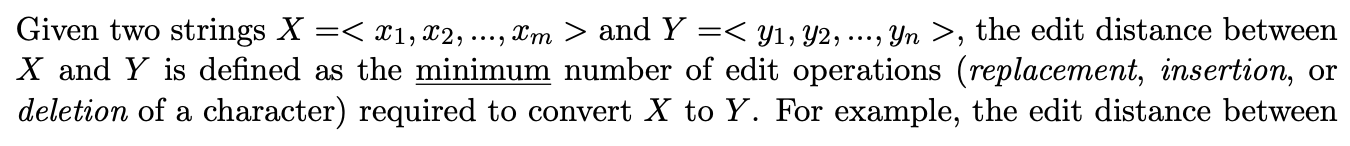
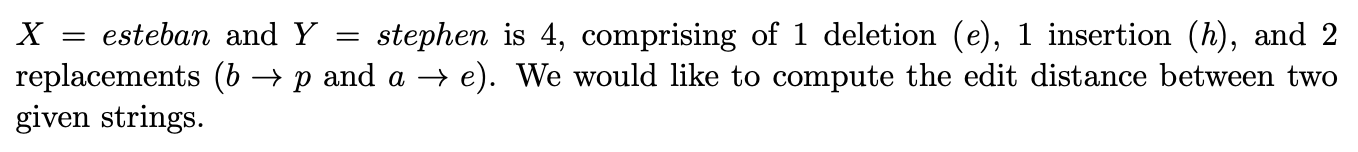
Given two strings X = and Y =, the edit distance between X and Y is defined as the minimum number of edit operations (replacement, insertion, or deletion of a character) required to convert X to Y. For example, the edit distance between X esteban and Y stephen is 4, comprising of 1 deletion (e), 1 insertion (h), and 2 replacements (b + p and a +e). We would like to compute the edit distance between two given strings. Steps: (i) Identify the last question you need to answer in developing a solution. *(ii)* Define and prove optimal substructure. (iii) Define subproblems, express the solution to the overall problem in terms of the subproblems. (iv) Formulate a recursive solution to the subproblems. Do not forget to specify the base case(s). (v) Characterize the runtime of the resulting procedure assuming that you would implement your solution using a bottom-up procedure. *(vi)* Provide the pseudo code of the bottom-up procedure you use to compute the value of the optimal solution, as well as the procedure for reconstructing the optimal solution. Given two strings X = and Y =, the edit distance between X and Y is defined as the minimum number of edit operations (replacement, insertion, or deletion of a character) required to convert X to Y. For example, the edit distance between X esteban and Y stephen is 4, comprising of 1 deletion (e), 1 insertion (h), and 2 replacements (b + p and a +e). We would like to compute the edit distance between two given strings. Steps: (i) Identify the last question you need to answer in developing a solution. *(ii)* Define and prove optimal substructure. (iii) Define subproblems, express the solution to the overall problem in terms of the subproblems. (iv) Formulate a recursive solution to the subproblems. Do not forget to specify the base case(s). (v) Characterize the runtime of the resulting procedure assuming that you would implement your solution using a bottom-up procedure. *(vi)* Provide the pseudo code of the bottom-up procedure you use to compute the value of the optimal solution, as well as the procedure for reconstructing the optimal solution