Question: i) Show that f(x) is the solution of the equation. ii) Solve this equation. = = = f(t) sin a(z - t)dt fonksiyonunun, a y

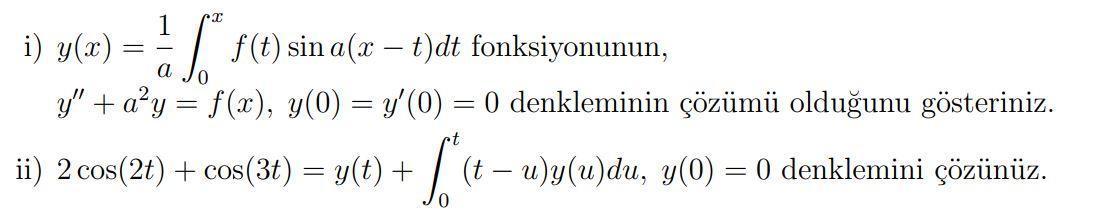
= i) y(x) y + aʻy = f(x), y(0) = y(0) = 0 denkleminin çözümü olduğunu gösteriniz. аra $*s(t) sin a(x – tydt fonksiyonunun, [

i) Show that f(x) is the solution of the equation.

ii) Solve this equation.

= = = f(t) sin a(z - t)dt fonksiyonunun, a y" + ay = f(x), y(0) = y'(0) = 0 denkleminin zm olduunu gsteriniz. ii) 2 cos (2t) + cos(3t) = y(t) + [* (t u)y(u)du, y(0) = 0 denklemini znz. i) y(x)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

SOLUTION i lk olarak verilen denklemi kontrol etmek iin yxi fxe eitleyelim yx ft sinaz t dt yx ft si... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Economics Questions!

If a sum of $9257 is deposited now, $1374 two years from now, and $1375 per year in years 6 through 10, the amount in year 10 at an interest rate of 10% per year will be closest to: O a. $35350 O b....

Suppose after submitting your sealed bid in a Vickrey auction you find out that you have lost the auction (you were not the highest bidder); however, you have the opportunity to revise your bid....

The bidders in a Dutch auction are as follows: The number of shares being auctioned is 210,000. What is the price paid by investors? How many shares does each investor receive? Bidder Number of...

TJ runs a side business called TJ's Tikoy Shop that becomes busy every year around the New Year selling tikoy (rice cakes/). To prepare for the rush, he hires extra staff to help fill the order. Each...

(a) Use the analogy between Faraday's law and Ampere's law, together with the Biot-Savart law, to show that for Faraday-induced electric fields. (b) Referring to Prob. 5.50a, show that where A is the...

Continuum ware equation show that for long wavelengths the equation of motion (2) reduces to the continuum elastic wave equation where v is the velocity of sound 02 x

a. On the same set of axes sketch the graphs of b. Write down the number of real solutions to the equation 4/x 2 = 3x + 7. c. Show that you can rearrange the equation to give (x + 1)(x + 2)(3x 2) =...

Show that for any angle , the equation x 2 + y 2 = r 2 becomes (x) 2 + (y) 2 = r2 when the rotation of axes formulas are applied.

Show that y = x 2 /4c is the equation of a parabola with directrix y = c, focus (0, c), and the vertex at the origin, as stated in Theorem 3. THEOREM 3 Parabola in Standard Position Let c#0. The...

7. In rectangular coordinates the equation of the hyperbola shown in the figure is given by: (a) Use MATLAB to show that in parametric form the equation of the hyperbola can be written as: and (b)...

Practical Application: List the pros and cons of raising the minimum wage.

Which of these will increase the present value of an amount tobe received sometime in the future? Increase in the time until theamount is received. Decrease in the futurevalue. Decrease in both the...

what i s x 2 - x + 5 ( x - 2 ) ( x - 1 ) ( x + 3 ) d x ?

For the circuit shown in Fig. 19-65, determine (a) The current through the 14-V battery and (b) The potential difference between points a and b, Va Vb. 15 ka b 10 k2 18 V 20 k2 14 V 12V ww-

The circuit in Figure P28.37 has been connected for a long time. (a) What is the voltage across the capacitor? (b) If the battery is disconnected, how long does it take the capacitor to discharge to...

An engine oil cooler consists of a bundle of 25 smooth tubes, each of length L = 2.5 m and diameter D = 10 mm. (a) If oil at 300 K and a total flow rate of 24 kg/s is in fully developed flow through...

The values of the components in a simple series RC circuit containing a switch (Fig. 28.19) are C = 1.00 F, R = 2.00 x 106 , and Є= 10.0 V. At the instant 10.0 s after the switch is closed,...

Suppose the fractional efficiency of a cesium surface (with work function 1.80eV) is 1.0 x 10 -16 that is, on average one electron is ejected for every 10 16 photons that reach the surface. What...

19 of 20 What are some of the tasks of the discussion leader during the guided discussion? Select all that apply. Interject appropriate material from prior discussions Select appropriate training...

2. (10 points) Find the absolute maximum and absolute minimum values of f on the given inter- val. (Show process! No process - No credit!) f (x) = In(x2 - 2x + 6), [-1, 2] Value! Abs. Max Value is: (...

2.14 More on expected value Because the expected value concept plays an important role in many economic theories, it may be useful to summarise a few more properties of this statistical measure....

can someone please help me with this questionPlease be specific with your solutionThanks a lot Question 1. Consider the second order partial differential equation 20zu at2 (1) for an unknown...

Please # 3 , 7, 11 , 15 1. If the radius of convergence of the power series _,=( Cnx" 17-22 Find a power series representation for the function and is 10, what is the radius of convergence of the...

1. (1 point) Find the value of the constant c that makes the 5. (1 point) Find a value of the constant &, if possible, at following function continuous on (-,). which f(s ) = cs+9 ifse (-, 8] f (x )...

For the function f use composition of functions to show that 5 7 1 x 7x 1 x 3x 7x 1 is as given 7 To show that f x x find f of x and 1 of x and check to see that each is x only f o f x is is x each...