Provide an octave code to the following problem. The final answer must be 1.5 hours.

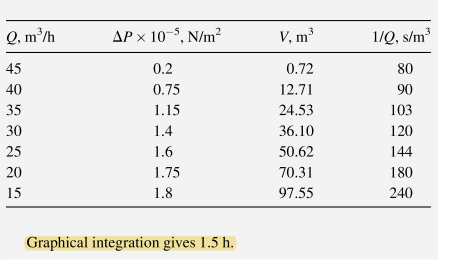
Tests conducted on a laboratory plate-and-frame filter produced the data given below. Determine the time required to process 50m3 of the same filtrate in a filter press with an area of 50m2, using the same cloth and filter aid as the laboratory unit. Data: c=2,710kg/m3; medium resistance, Rm=6.4621010/m; filtrate viscosity, =2.78107Nh/m2;cF=10.037kg/m3; =1.0691011m/kg. Solution The pump characteristic curve, Figure 19.25, shows the pump discharge pressure, as a function of volumetric flow rate through the pump, Q. Assume the flow rate is the filtrate, where Q=dV/dt. The time required for a volume of filtrate, V, is t=0VQdV which can be numerically integrated as follows. Assume the P across the filter medium and cake in bar = the discharge pressure of the pump in barg. Rearrange the Darcy equation, (19-22), so that V is a function of Q : Q=AcP/[Rm+acF(V/Ac)] Solving for V, V=cFAc[QAcPRm] Thus, using SI units, V==2.78107(1.0691011)(10.037)50[Q50(P)2.78107(6.4621010)]0.00838[P/Q359] Using the pump characteristic curve of Figure 19.25, tabulate Q, P,V from (4), and 1/Q starting from Q=45m3/h and marching down in increments of 5m3/h. Then plot 1/Q versus V until it just exceeds 50m3/h. From (1), by graphical integration, the area under the curve from V=0 to 50m3/h, as shown in Figure 19.26, is equal to the filtration time. Figure 19.26 Graphical integration for Example 19.9. Graphical integration gives 1.5h