provide answer asap

solved example is

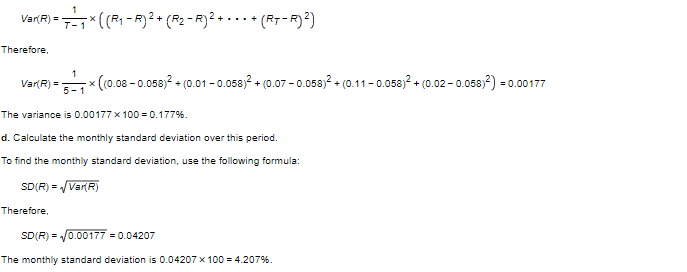
Consider the following five monthly returns: a. Calculate the arithmetic average monthly return over this period. b. Calculate the geometric average monthly return over this period. c. Calculate the monthly variance over this period. d. Calculate the monthly standard deviation over this period. a. Calculate the arithmetic average monthly return over this period. The arithmetic average is \%. (Round to two decimal places.) Consider the following five monthly returns: a. Calculate the arithmetic average monthly return over this period. b. Calculate the geometric average monthly return over this period. c. Calculate the monthly variance over this period. d. Calculate the monthly standard deviation over this period. a. Calculate the arithmetic average monthly return over this period. To find the arithmetic average, use the following formula: R=T1(R1+R2++RT) Therefore, R=51(0.08+0.01+0.07+0.11+0.02)=0.058 The arithmetic average is 0.058100=5.80%. b. Calculate the geometric average monthly return over this period. To find the geometric average, use the following formula: R=((R1+1)(R2+1)(RT+1))T11 Therefore, b. Calculate the geometric average monthly return over this period. To find the geometric average, use the following formula: R=((R1+1)(R2+1)(RT+1))T1 Therefore, R=(1.081.011.071.111.02)51=0.057330 The geometric average is 0.057330100=5.733%. c. Calculate the monthly variance over this period. To find the variance, use the following formula: Var(R)=T11((R1R)2+(R2R)2++(RTR)2) Therefore, Var(R)=511((0.080.058)2+(0.010.058)2+(0.070.058)2+(0.110.058)2+(0.020.058)2)=0.00177 The variance is 0.00177100=0.177% d. Calculate the monthly standard deviation over this period. To find the monthly standard deviation, use the following formula: Var(R)=T11((R1R)2+(R2R)2++(RTR)2) Therefore, Var(R)=511((0.080.058)2+(0.010.058)2+(0.070.058)2+(0.110.058)2+(0.020.058)2)=0.00177 The variance is 0.00177100=0.177%. d. Calculate the monthly standard deviation over this period. To find the monthly standard deviation, use the following formula: SD(R)=Var(R) Therefore, SD(F)=0.00177=0.04207 The monthly standard deviation is 0.04207100=4.207%