Provide code in python

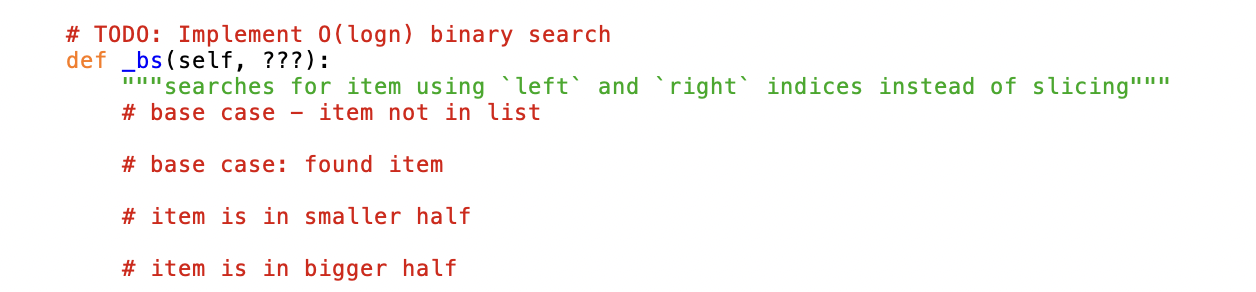
Mod 6 Lab - Ordered List ADT The Ordered List ADT is similar to a list, but adds the requirement that items remain sorted: - add( item) - adds item to the list. - remove(item) - removes the first occurrence of item from the list. Raise a RuntimeError if the item is not present. - getitem(index) - returns the item with the given index in the sorted list. This is also known as selection. - contains(item) - returns True iff there is an item of the list equal to item. - iter - returns an iterator over the ordered list that yields the items in sorted order. - len - returns the length of the ordered list. We have provided a working Ordered List in lab6.py. The starter code includes 3 ways of implementing contains: -_bs (???) - up to you to implement. Should be O(logn). - _contains_list(item) - uses python's built-in list search. O(n). - contains_bs_slow (item) - uses a binary search built on slicing. O(n). def __contains__(self, item): return self._bs(item, 0, len(self)) \#Requires_bs() for this to work \# alternative search algorithms: \# return self._contains_list(item) \# uses python's default list-search \# return self._contains_bs_slow(item) \# uses a slow version of binary-search (slicing) Deliverable - _bs() Implement a O(logn) binary search. You'll need to pass left/right indices insted of list slices with each recursive call to do this. Note that TesetLab6.py, included with the starter code, tests the contains method. If you are struggling to debug with the tests provided, try writing your own. Submission At a minimum, submit the following files: - lab6.py Students must submit individually by the due date (typically, Sunday at 11:59 pm EST) to receive credit. \# TODO: Implement o(logn) binary search def _s(self, ???): \#"Isearches for item using 'left' and 'right' indices instead of slicing" \# base case - item not in list \# base case: found item \# item is in smaller half \# item is in bigger half