Provide the solution of the 2 problems, the answer was given in the right side of the given:

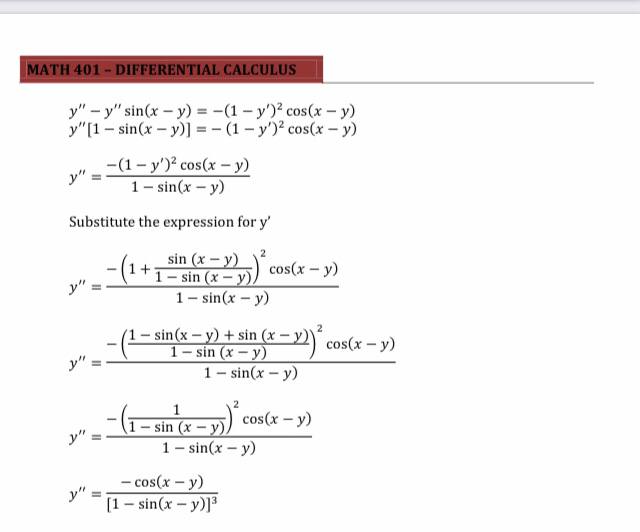
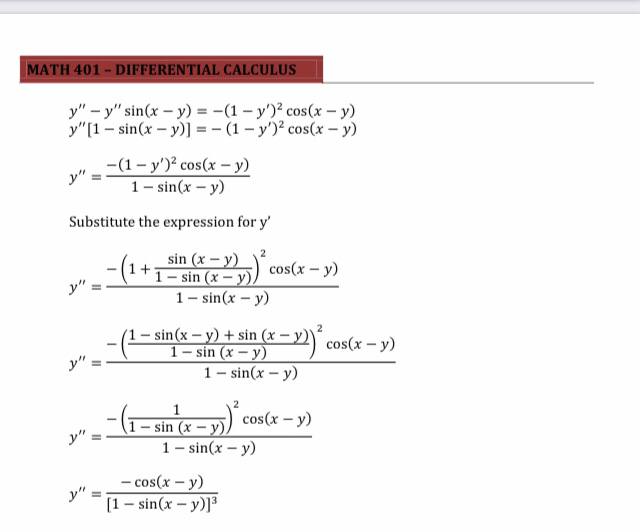
Use implicit differentiation to find the 9. y' of sec2x + csczy = 9 tan x sec2x ans. y'= coty csczy 10.y" of sin x + cosy = 1 ans. y' = sinxsin2y-cos2xcosy sinBy3.1.4. Implicit Differentiation of Trigonometric Functions In this section, we will apply the process of implicit differentiation for equations involving trigonometric functions. Implicit differentiation is a technique based on a Chain Rule that is used to find the derivative when the relationship between the variables is given implicitly rather than explicitly (solved for one variable in terms of the other). Example 3.1.4.1 Find the y' given that (a) x cosy + y cos x - 4 = 0. Solution: Since it is difficult to express y in terms of x only, we will differentiate implicitly with respect to x. (x)(-siny) " + (cos y) #+ (y) (cos x) + (cosx) => - (4) = 0 (-xsiny)y' + (cosy)(1) + (y)(-sin x) + (cosx)y' -0 =0 y'(-xsiny + cosx) = y sinx - cosy y sinx - cosy cos x - x sin y (b)tan(xy) + xy = 0 Solution: Since it is difficult to express y in terms of x only, we will differentiate implicitly with respect to x. dy dx sec'(xy) dx (xy)+xduty = 0 dy dx dy dx sec'(xy) |* +yat*dx -+ydx =0 sec'(xy) [xy' + y(1)] + xy' + y(1) = 0 y'x sec?(xy) + ysec?(xy) + xy'ty = 0 y'xsec'(xy) + xy' = - ysec?(xy) -y y'x [sec?(xy) + 1] = - y [sec?(xy) + 1] y y[sec(xy) + 1] x[sec2(xy) + 1]MATH 401 - DIFFERENTIAL CALCULUS Example 3.1.4.2 Find the y" given that (a) tan(xy) + xy = 0 Solution : Using the result of y' of the Example 3.1.4.1 (b), we can evaluate the 2nd derivative y" as follows y' X xy' = -y By implicit differentiation with respect to x, we have d dx dy Tyty ax xy"+y() = -y ry'= -2y -2y' X Substitute the expression of y' -2 X X x2 (b) y = cos (x - y) Solution: Start with the implicit differentiation with respect to x dy -= -sin (x - y) - (x -y) d dx dx y' = - sin(x - y) + y'sin (x - y) dx dy y = -sin (x - y) y'[1 - sin(x - y)] = -sin (x - y) dx -sin (x - y) y' = - sin(x - y) (1 -y') y' 1 - sin (x - y) To evaluate the y", perform another implicit differentiation with respect to x. Use Product Rule on the right side. d dx = - sin(x - y)7 -(1-y')+ (1-y')= [- sin(x - y)] y" = - sin(x - y) (0 - y') + (1 - y')[- cos(x - >)] 7 (x -y) y" = y" sin(x - y) + (1 - y')[- cos(x - y)](1 - y')MATH 401 - DIFFERENTIAL CALCULUS y"- y" sin(x - y) = -(1 - y') cos(x - y) y"[1 - sin(x - y)] = - (1 - y') cos(x - y) y " -(1-y') cos(x - y) 1 - sin(x - y) Substitute the expression for y' (1+ sin (x - y) 1 - sin (x - y) cos(x - y) y" 1 - sin(x - y) - sin(x - y) + sin (x - y) 2 1 - sin (x - y) cos(x - y) 1 - sin(x - y) - sin (x - y) cos(x - y) 1 - sin(x - y) - cos(x - y) y' [1 - sin(x - y)]3