Question: provided the theorems needed also Consider a linear model with only categorical predictors, written in matrix form as y = X1B, + E1. Suppose we

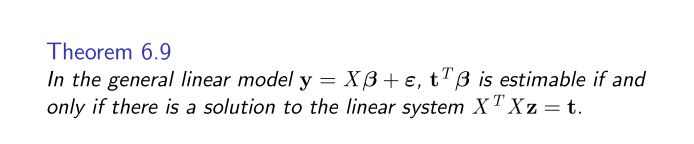
provided the theorems needed also


![It? ] is partitioned according to the categorical and continuous predictors. Show](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66783b58a96f4_54466783b588c8cd.jpg)
Consider a linear model with only categorical predictors, written in matrix form as y = X1B, + E1. Suppose we add some continuous predictors, resulting in an expanded model y = XB +e. Now consider a quantity toB, where to = [t; It? ] is partitioned according to the categorical and continuous predictors. Show that if t. B, is estimable in the first model, then to B is estimable in the second model. If you write X = [X1 X2], you may assume that r(X) = r(X1) +r(X2). Hint: Use Theorems 6.9 and 6.3. For any vectors z1 and z2, you can write XX1 XTX2 XXIZI XT 0 X1 X2 X1Z1 X2 X1 X2 X2 X2 X2z2 0 X1 X2 X272Theorem 6.3 The system Ax = g is consistent if and only if the rank of [ A | g ] is equal to the rank ofA.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


