Pseudocode Pg 47:

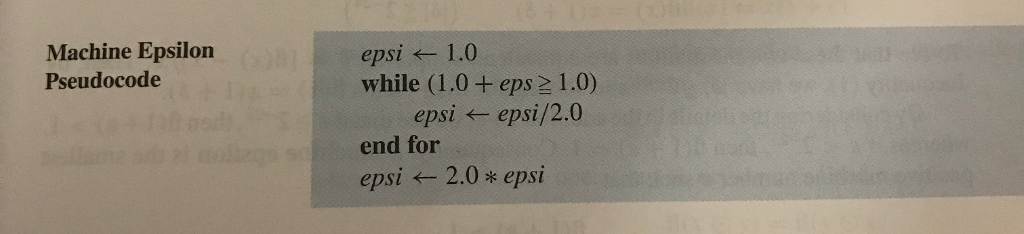
Machine Epsilon Pseudocode epsi leftarrow 1.0 while (1.0 + eps greaterthanorequalto 1.0) epsi leftarrow epsi/2.0 end for epsi leftarrow 2.0 * epsi MATLAB has a built-in machine epsilon, which is the precision to which a number can be represented. The default machine epsilon is for a double-precision floating point number (and we will use double-precision as our default) and is stored in eps. MATLAB has other machine precisions you can also call and you can explore in the documentation. This is different than the smallest number that can be represented in MATLAB, which is stored in realmin. There is an analogous largest number realmax. (a) Write a loop that starts at x = 1 and tries to find the distance between x and the next largest discernible machine number. (See the pseudocode on page 47.) (b) How does the distance in part (a) compare to eps? (c) Write a loop that starts at x = 1 and uses divisions by two to determine the smallest number you can represent in MATLAB. (d) Does the number you find equal realmin? Explain any differences you notice. What does this mean for numbers that are between MATLAB's smallest number and the number you find? (e) Write a loop that starts at x = 1 and use multiplication by 2 to try to determine the largest number you can represent in MATLAB. (f) Does the number you find equal realmax? Explain any differences you notice. If you didn't get exactly realmax, try to adjust the code to obtain it. Note any adjustments you made (just assigning the value of realmax or similar artificial forcing don't count.) Machine Epsilon Pseudocode epsi leftarrow 1.0 while (1.0 + eps greaterthanorequalto 1.0) epsi leftarrow epsi/2.0 end for epsi leftarrow 2.0 * epsi MATLAB has a built-in machine epsilon, which is the precision to which a number can be represented. The default machine epsilon is for a double-precision floating point number (and we will use double-precision as our default) and is stored in eps. MATLAB has other machine precisions you can also call and you can explore in the documentation. This is different than the smallest number that can be represented in MATLAB, which is stored in realmin. There is an analogous largest number realmax. (a) Write a loop that starts at x = 1 and tries to find the distance between x and the next largest discernible machine number. (See the pseudocode on page 47.) (b) How does the distance in part (a) compare to eps? (c) Write a loop that starts at x = 1 and uses divisions by two to determine the smallest number you can represent in MATLAB. (d) Does the number you find equal realmin? Explain any differences you notice. What does this mean for numbers that are between MATLAB's smallest number and the number you find? (e) Write a loop that starts at x = 1 and use multiplication by 2 to try to determine the largest number you can represent in MATLAB. (f) Does the number you find equal realmax? Explain any differences you notice. If you didn't get exactly realmax, try to adjust the code to obtain it. Note any adjustments you made (just assigning the value of realmax or similar artificial forcing don't count.)