Question: public class Complex implements Comparable , Cloneable{ private double realPart; private double imaginary; private final double DELTA = 0.000001; public Complex() { this.realPart = 0;
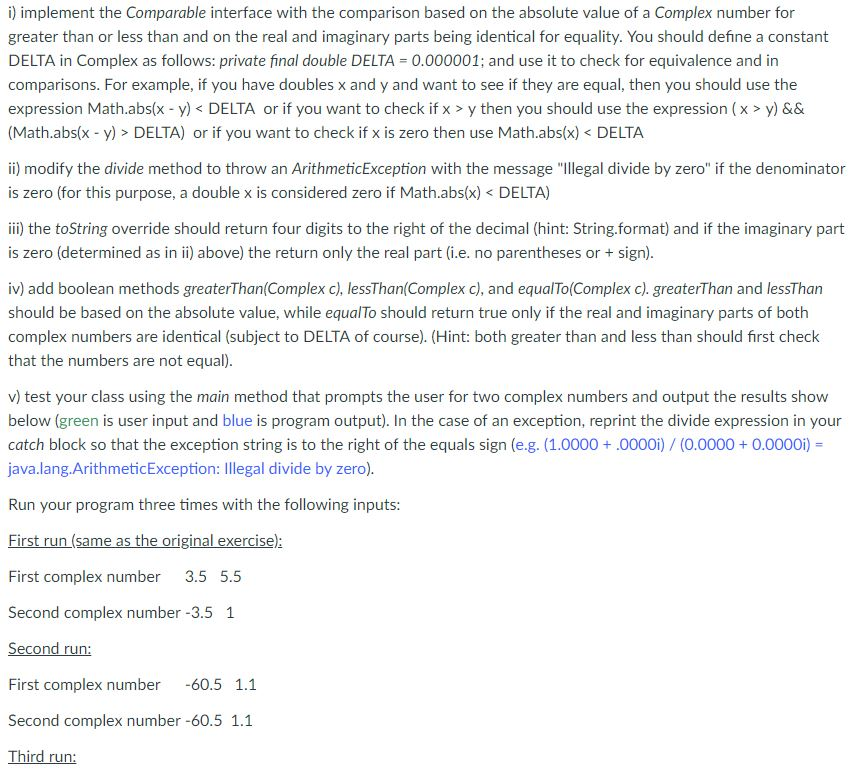

public class Complex implements Comparable
private double realPart; private double imaginary; private final double DELTA = 0.000001;
public Complex() { this.realPart = 0; this.imaginary = 0; }
public Complex(double realPart) { this.realPart = realPart; this.imaginary = 0; }
public Complex(double realPart, double imaginary) { this.realPart = realPart; this.imaginary = imaginary; }
public Complex add(Complex c) { Complex result = new Complex(this.getRealPart() + c.getRealPart(), this.getImaginary() + c.getImaginary()); return result; }
public Complex subtract(Complex c) { Complex result = new Complex(this.getRealPart() - c.getRealPart(), this.getImaginary() - c.getImaginary()); return result; }
public Complex multiply(Complex c) { double real = (this.getRealPart() * c.getRealPart()) - (this.getImaginary() * c.getImaginary()); double img = (this.getRealPart() * c.getImaginary()) + (this.getImaginary() * c.getRealPart()); Complex result = new Complex(real, img); return result; }
public Complex divide(Complex c) { if(c.abs()
Complex result = new Complex(real, img); return result; } public double abs() { return Math.sqrt(Math.pow(getRealPart(), 2) + Math.pow(getImaginary(), 2)); } public double getRealPart() { return realPart; }
public double getImaginary() { return imaginary; }
public boolean greaterThen(Complex c) { if(equalTo(c)) return false; if((Math.abs(this.getRealPart() - c.getRealPart()) > DELTA && Math.abs(this.getImaginary() - c.getImaginary()) > DELTA) && (this.abs() > c.abs())) return true; return false; }
public boolean lessThen(Complex c) { if(equalTo(c) || greaterThen(c)) return false; return true; }
public boolean equalTo(Complex c) { if(Math.abs(Math.abs(this.getRealPart()) - Math.abs(c.getRealPart()))
@Override public int compareTo(Complex c) { if(equalTo(c)) return 0; if(greaterThen(c)) return 1; return -1; }
@Override public Complex clone() { Complex cloneObject = new Complex(this.getRealPart(), this.getImaginary()); return cloneObject; }
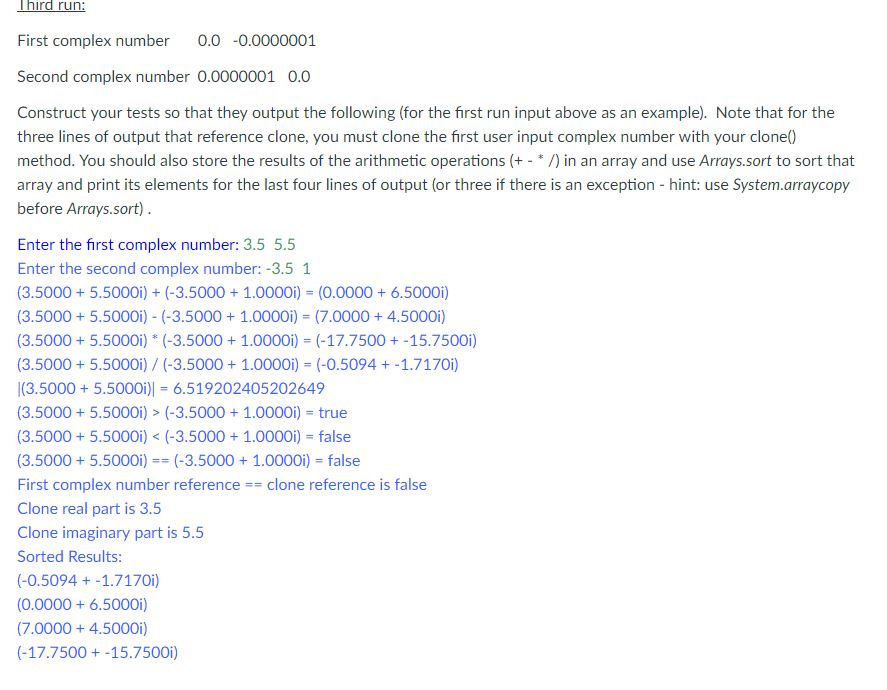
@Override public String toString() { String realPartString = String.format("(%.4f", getRealPart()); if(Math.abs(getImaginary()) private void printBasicOperationalValue(String a, String b, String c, String operation) { StringBuilder sb = new StringBuilder(); sb.append(a); sb.append(operation); sb.append(b); sb.append(" = "); sb.append(c); System.out.println(sb.toString()); } private void printBasicOperationalValue(String a, String b, boolean c, String operation) { StringBuilder sb = new StringBuilder(); sb.append(a); sb.append(operation); sb.append(b); sb.append(" = "); sb.append(c); System.out.println(sb.toString()); } public void printAbsoluteValue() { System.out.println("|" + this.toString() + "| = " + this.abs()); } public void cloneOperation() { Complex clonedObject = this.clone(); System.out.println("First complex number reference == clone reference is " + (this == clonedObject)); System.out.println("Clone real part is " + clonedObject.getRealPart()); System.out.println("Clone imaginary part is " + clonedObject.getImaginary()); } private void sortedResults(Complex[] src, int len) { Complex[] dest = new Complex[len]; System.arraycopy(src, 0, dest, 0, len); Arrays.sort(dest); System.out.println("Sorted Result: "); for(Complex complex : dest) { System.out.println(complex.toString()); } } public void performComplexOperation(Complex c) { Complex[] complexes = new Complex[4]; int resultIndex = 0; complexes[resultIndex] = add(c); printBasicOperationalValue(this.toString(), c.toString(), complexes[resultIndex++].toString(), " + "); complexes[resultIndex] = subtract(c); printBasicOperationalValue(this.toString(), c.toString(), complexes[resultIndex++].toString(), " - "); complexes[resultIndex] = multiply(c); printBasicOperationalValue(this.toString(), c.toString(), complexes[resultIndex++].toString(), " * "); try { complexes[resultIndex] = divide(c); printBasicOperationalValue(this.toString(), c.toString(), complexes[resultIndex++].toString(), " / "); } catch (ArithmeticException exception) { printBasicOperationalValue(this.toString(), c.toString(), "java.lang.ArithmeticException: " + exception.getMessage(), " / "); } printAbsoluteValue(); boolean greaterThenResult = greaterThen(c); printBasicOperationalValue(this.toString(), c.toString(), greaterThenResult, " > "); boolean lessThenResult = lessThen(c); printBasicOperationalValue(this.toString(), c.toString(), lessThenResult, " public static void main(String[] args) { Scanner scanner = new Scanner(System.in); System.out.printf("Enter the first complex number: "); Complex firstComplexNumber = new Complex(scanner.nextDouble(), scanner.nextDouble()); System.out.printf("Enter the second complex number: "); Complex secondComplexNumber = new Complex(scanner.nextDouble(), scanner.nextDouble()); firstComplexNumber.performComplexOperation(secondComplexNumber); } }
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


