python code

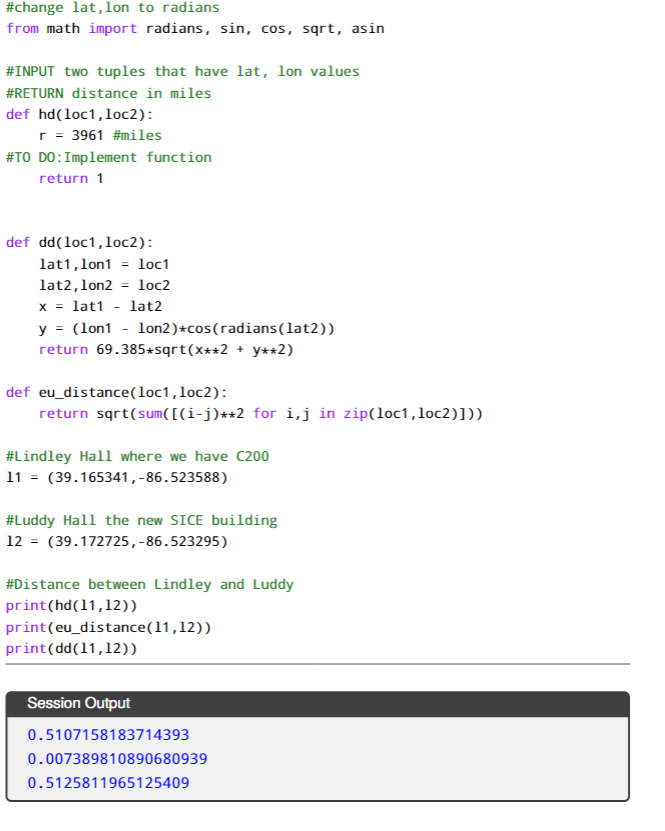
Finding the distance between two points P1 = (Pny), P2-(x2M), d(P1, P2) in a 2D plane is straightforward: When calculating the distance on the Earth, however, we have to take into account Earth's shape. To that end, we can use the Haversine formula, named by Inman for the function called the haversin. If pi,p2 are on a Earth (sphere) we have where d is the distance between the points for a sphere whose radius is r. To solve for d we take the inverse sin and muliply by r d2r arcsin((h Assume the points Pi,P2 are latitude, longitude pairs. These pair describe a point through intersection: The latitude runs parallel to the equator and longitude runs perpendicular to the equator. They intersect at a point. We now show how to calculate distance between two points on the Earth using P1 = (lah, lon 1), P2 = (lat2, lona) latitude and longitude latz -lat 2 on2Lon 2 lond doin(lata)2+cos(la)(lat2)sin(lond) r3961 mi. When implementing in Python, you'll have to make sure to convert to radians. arcsin is imple- mented in math as asin0 Finding the distance between two points P1 = (Pny), P2-(x2M), d(P1, P2) in a 2D plane is straightforward: When calculating the distance on the Earth, however, we have to take into account Earth's shape. To that end, we can use the Haversine formula, named by Inman for the function called the haversin. If pi,p2 are on a Earth (sphere) we have where d is the distance between the points for a sphere whose radius is r. To solve for d we take the inverse sin and muliply by r d2r arcsin((h Assume the points Pi,P2 are latitude, longitude pairs. These pair describe a point through intersection: The latitude runs parallel to the equator and longitude runs perpendicular to the equator. They intersect at a point. We now show how to calculate distance between two points on the Earth using P1 = (lah, lon 1), P2 = (lat2, lona) latitude and longitude latz -lat 2 on2Lon 2 lond doin(lata)2+cos(la)(lat2)sin(lond) r3961 mi. When implementing in Python, you'll have to make sure to convert to radians. arcsin is imple- mented in math as asin0