python code

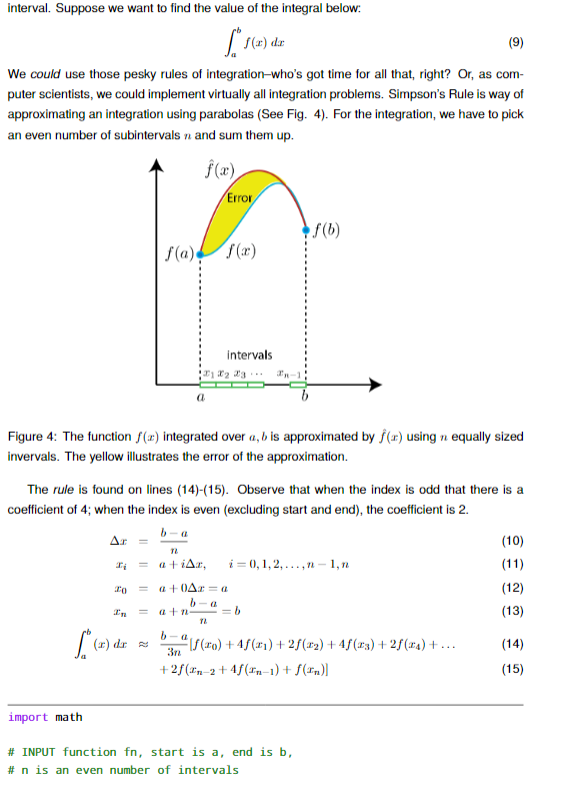
output

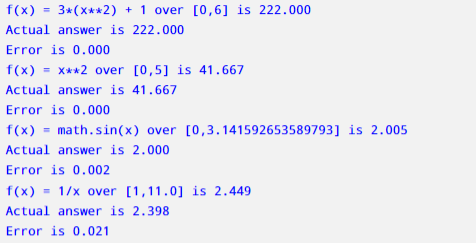
interval. Suppose we want to find the value of the integral below: f(x) dz We could use those pesky rules of integration-who's got time for all that, right? Or, as com- puter scientists, we could implement virtually all integration problems. Simpson's Rule is way of approximating an integration using parabolas (See Fig. 4. For the integration, we have to pick an even number of subintervals n and sum them up. f(a) rror f(b) (a(r)i :intervals Figure 4: The function f() integrated over a,b is approximated by(r) usingn equally sized invervals. The yellow illustrates the error of the approximation. The rule is found on lines (14)-(15). Observe that when the index is odd that there is a coefficient of 4; when the index is even (excluding start and end), the coefficient is 2 1 (10) T& (12) (13) (14) (15) T& (r) dr import math # INPUT function fn, start is a, end is b, # n is an even number of intervals interval. Suppose we want to find the value of the integral below: f(x) dz We could use those pesky rules of integration-who's got time for all that, right? Or, as com- puter scientists, we could implement virtually all integration problems. Simpson's Rule is way of approximating an integration using parabolas (See Fig. 4. For the integration, we have to pick an even number of subintervals n and sum them up. f(a) rror f(b) (a(r)i :intervals Figure 4: The function f() integrated over a,b is approximated by(r) usingn equally sized invervals. The yellow illustrates the error of the approximation. The rule is found on lines (14)-(15). Observe that when the index is odd that there is a coefficient of 4; when the index is even (excluding start and end), the coefficient is 2 1 (10) T& (12) (13) (14) (15) T& (r) dr import math # INPUT function fn, start is a, end is b, # n is an even number of intervals