python: errors need help with

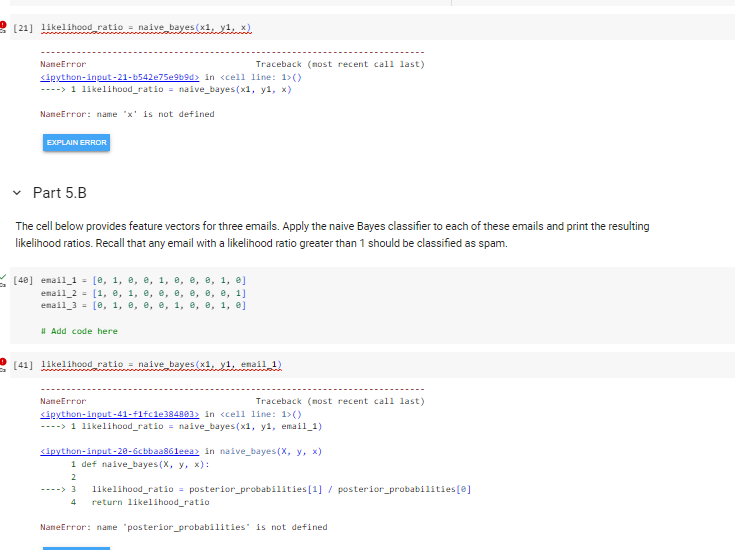
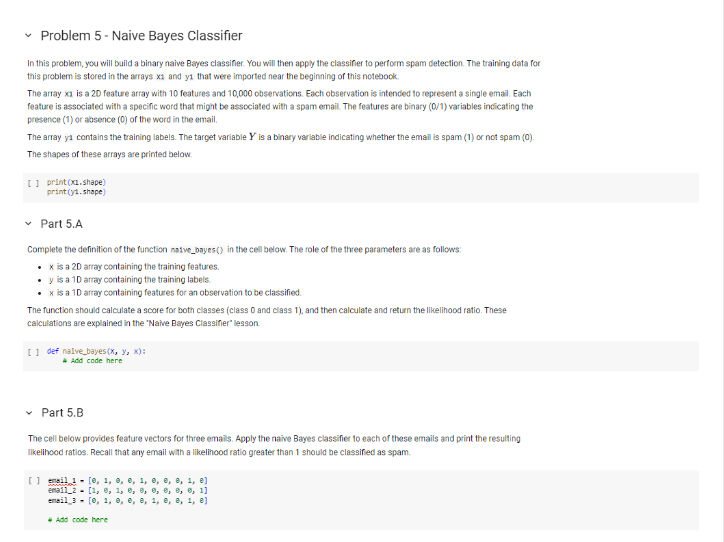
Problem 5 - Naive Bayes Classifier In this problem, you will build a binary naive Bayes classiner. You will then apply the classiner to perform spam detection. The training data for this problem is stored in the arrays x1 and y1 that were imported near the beginning of this notebock. The array x1 is a 20 feature array with 10 features and 10,000 observations. Each observation is intended to represent a single emai. Each feature is associated with a specific word that might be associated with a spam email. The features are binary (0/1) variables incicating the presence (1) or absence ( 0 ) of the word in the email. The array y1 contains the training labels. The target variable Y is a binary variable indicating whether the email is spam (1) or not spam (0). The shapes of these arrays are printed below. [. ] print(x1.shape) print (y1.shape) Part 5.A Complete the definition of the function noive_boyes (y in the cell below. The fole of the three parameters are as follows: - x is a 20 array containing the training features. - y is a 10 array containing the training labels. - x is a 10 array containing features for an observation to be classified. The function should calculate a score for both classes (class 0 and class 1), and then calculate and return the likelihood ratio. These calculations are explained in the "Nawe Bayes Classifler" lesson. [. ] def nalve_bayes (x,y,x) : 4 Add code here Part 5.B The cell below provides feature vectors for three emails. Apply the naive Bayes classifier to each of these emails and print the resulting likelihood ratios. Recall that any email with a likelinood ratio greater than 1 should be classifed as spam. [ ] \[ \begin{array}{l} \text { ensil } 1 \text { - }[\theta, 1, \theta, \theta, 1, \theta, \theta, \theta, 1, \theta] \\ \text { enail_2 - }[1,0,1,0, \theta, 0,0, \theta, 0,1] \\ \text { ensil_ } 3 \text { - }[\theta, 1, \theta, \theta, \theta, 1, \theta, \theta, 1, \theta] \\ \end{array} \] - Ads code here def naive_bayes (x,y,x) : \# Calculate the prior probabilities of each class P_class_0 = np.sum (y==0)/len(y) P_class_1 =npsum(y==1)/len(y) \# Calculate the likelihood probabilities for each feature likelihood_probabilities =nmeros((len(x[0]),2)) for i in range(len (x[])) : P_feature_given_class_ =npsum(x[:,i]&(y==0))psum(y==0) P_feature_given_class_1 =npsum(x[:,i]&(y==1))psum(y==1) likelihood_probabilities [i,0]= P_feature_given_class_ likelihood_probabilities [i,1] = P_feature_given_class_1 \# Calculate the posterior probabilities for each class posterior_probabilities =npzeros(2) for i in range(2): posterior_probabilities [i] = P_class_ 0 np.prod(likelihood_probabilities [:,i][x==1. posterior_probabilities /= np.sum(posterior_probabilities) \# Calculate and return the likelihood ratio likelihood_ratio = posterior_probabilities[1] / posterior_probabilities[0] return likelihood_ratio 1 likelihood_ratio = naive_bayes (x1,y1,x) NaneError Traceback (nost recent call last) Sipython-input-21-b542e75e9b9d> in () -..> 1 likelihood_ratio = naive_bayes (x1,y1,x) NaneError: name ' x ' is not defined Part 5.B The cell below provides feature vectors for three emails. Apply the naive Bayes classifier to each of these emails and print the resulting likelihood ratios. Recall that any email with a likelihood ratio greater than 1 should be classified as spam. [40] \[ \begin{array}{l} \text { enail_1 }=[\theta, 1, \theta, \theta, 1, \theta, \theta, \theta, 1, \theta] \\ \text { enail_2 }=[1, \theta, 1, \theta, \theta, \theta, \theta, \theta, \theta, 1] \\ \text { enail_3 }=[\theta, 1, \theta, \theta, \theta, 1, \theta, \theta, 1, \theta] \end{array} \] "I Add code here [41] 1ike1ihood ratio = naive bayes (x1,y1, enai1 1) NaneError Traceback (nost recent call last) Sipython-input-41-f1fc1e384893) in 1>() -.>> 1 likelihood_ratio = naive_bayes (x1,y1, email_1) Sipython-input-20-6cbbaa861eea> in naive_bayes( x,y,x) def naive_bayes (x,y,x) : 1ikelihood_ratio = posterior_probabilities[1] / posterior_probabilities[0] return 1ikelihood_ratio NaneError: name "posterior_probabilities" is not defined