Python: Fill your codes at the places marked xxx.

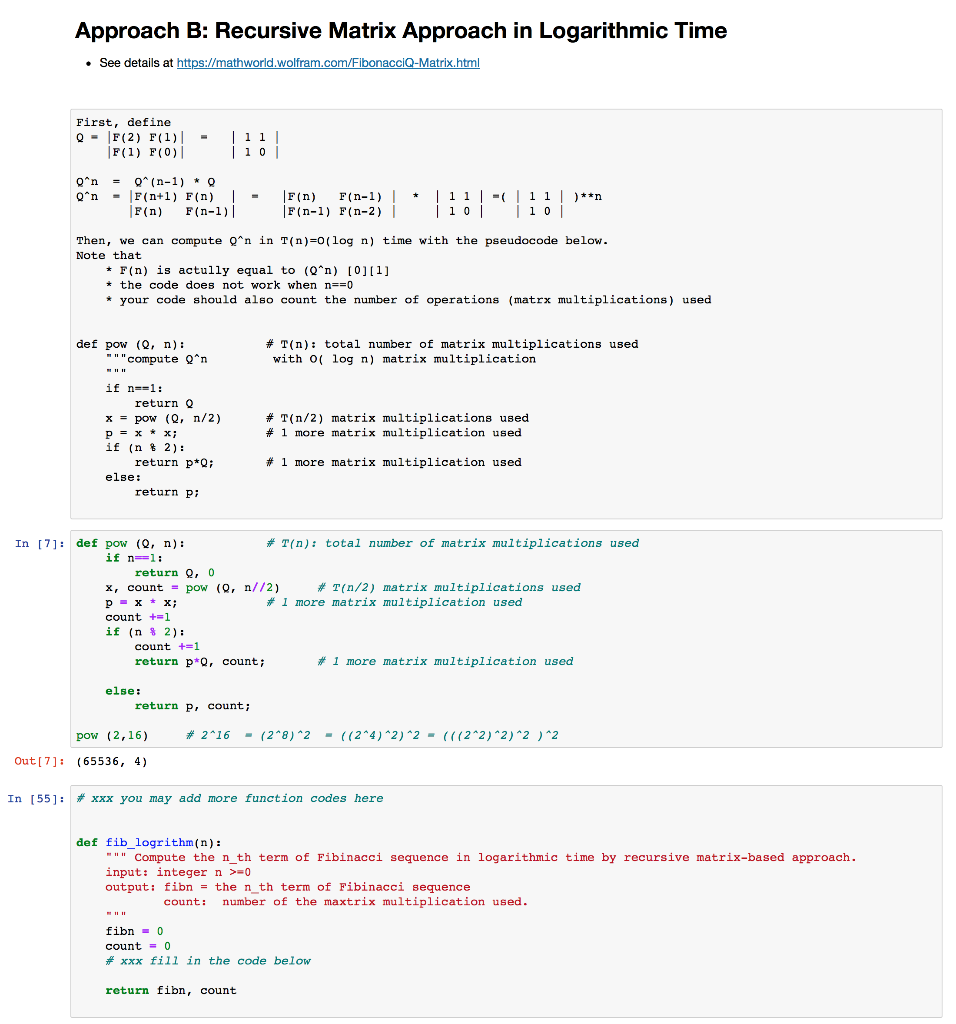
Approach B: Recursive Matrix Approach in Logarithmic Time See details at https://mathworld.wolfram.com/FibonacciQ-Matrix.html First, define Q = F(2) F(1) F(1) F(0)| | 11 | 10 * On (n-1) * Qn - F(n+1) F(n) | F(n) F(n-1) | | 11 - 11 )**n F(n) F(n-1) |F(n-1) F(n-2) | | 10 | | 10 Then, we can compute Qn in T(n)=0(log n) time with the pseudocode below. Note that * F(n) is actully equal to (Qn) [0][1] * the code does not work when n==0 * your code should also count the number of operations (matrx multiplications) used * def pow (Q, n): ""compute on # T(n): total number of matrix multiplications used with O( log n) matrix multiplication # T(n/2) matrix multiplications used # 1 more matrix multiplication used if n-1: return 0 x = pow (Q, n/2) P = x * X; if (n # 2): return p*Q; else: return Pi # 1 more matrix multiplication used In [7]: def pow (Q, n): # T(n): total number of matrix multiplications used if n=1: return Q, 0 x, count = pow (0, n//2) #T(n/2) matrix multiplications used p - X* X; # 1 more matrix multiplication used count +=1 if (n $ 2): count += 1 return p*Q, count; # 1 more matrix multiplication used else: return P, count; pow (2,16) #2416 - (28) 2 - ((2+4)*2)^2 = ((1242) 2) 2)2 Out[7]: (65536, 4) In [55]: xxx you may add more function codes here def fib_logrithm(n): " Compute the n_th term of Fibinacci sequence in logarithmic time by recursive matrix-based approach. input: integer n >=0 output: fibn = the n_th term of Fibinacci sequence count: number of the maxtrix multiplication used. fibn - 0 count = 0 # xxx fill in the code below return fibn, count