[PYTHON in Jupyter Notebook]

FIRST TWO PROBLEMS ARE FINISHED

I have the first two done correctly, but I need help on the second three! Thanks!!

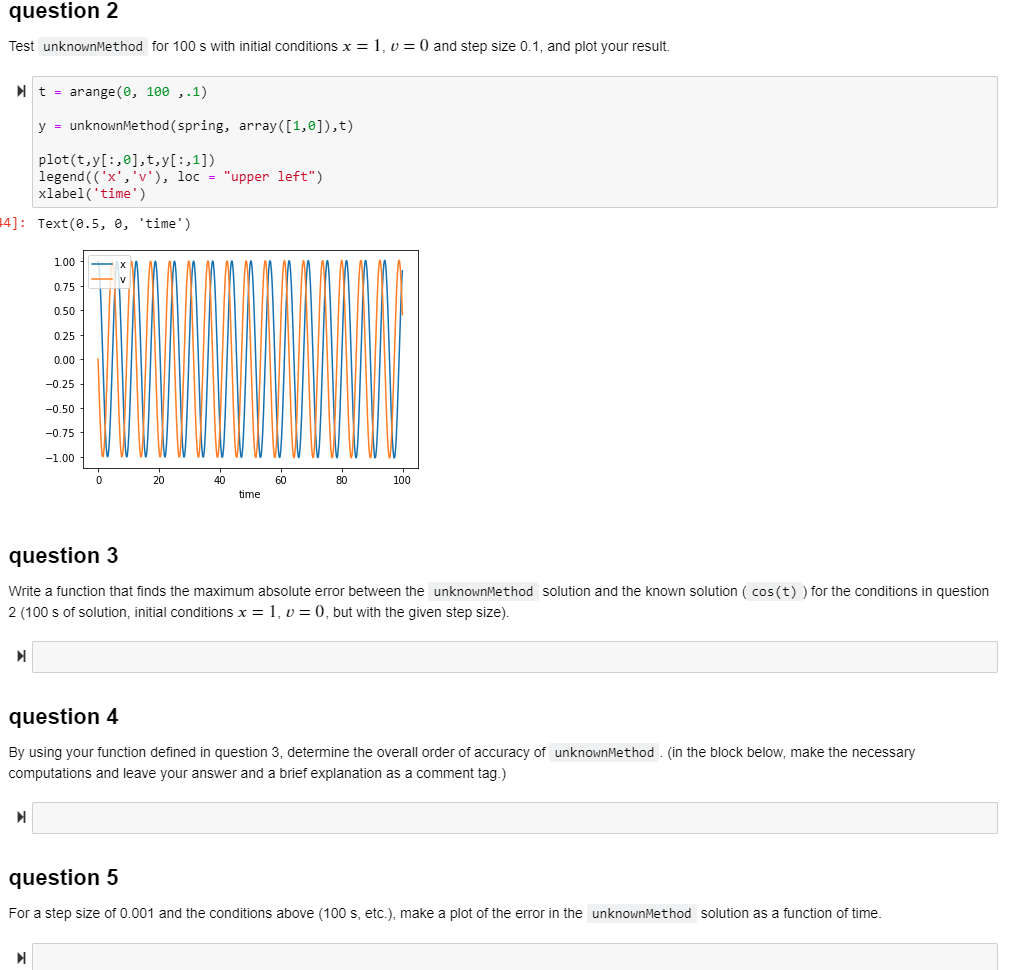
Analysis of yet another method for solving ODES In case you haven't realized, there are a lot of methods for solving ODEs, with various properties. This homework set asks you to analyze one of them to determine its order of accuracy and stability characteristics. Here's the method: : def unknownMethod(f,yo,t): npts = t. shape [0] y = np.zeros((npts, yo.shape[0])) y[0] = yo for i in range(0, npts-1): h = t[i+1]-t[i] k1 = f(y[i],t[i]) k2 = f(y[i]+2.0*h*k1/3.0,t[i]+2.0*h/3.0) y[i+1] = y[i] + h*(0.25*k1 + 0.75*2) return y This method is one of a class of very commonly-used ODE solvers called Runge-Kutta methods. question 1 Define a function describing the system of ordinary differential equations dx =U dt du k X m dt With klm = 1 s-2 (1.e. the mass-spring oscillator described in lecture) : def spring(y, t): x = y[0] V = y[1] k = m = 1 return array([v,(-k/m)*x]) question 2 Test unknownMethod for 100 s with initial conditions x = 1, 0 = 0 and step size 0.1, and plot your result. t = arange(0, 100 ,.1) y = unknownMethod(spring, array([1,0]),t) plot(t,y[:,0],t,y[:,1]) legend('x', 'v'), loc = "upper left") xlabel('time') 14]: Text(0.5, 0, 'time') 1.00 0.75 0.50 0.25 0.00 -0.25 -0.50 -0.75 -1.00 40 80 100 time question 3 Write a function that finds the maximum absolute error between the unknownMethod solution and the known solution ( cos(t)) for the conditions in question 2 (100 s of solution, initial conditions x = 1, v= 0, but with the given step size) question 4 By using your function defined in question 3, determine the overall order of accuracy of unknownMethod. (in the block below, make the necessary computations and leave your answer and a brief explanation as a comment tag.) question 5 For a step size of 0.001 and the conditions above (100 s, etc.), make a plot of the error in the unknownMethod solution as a function of time. Analysis of yet another method for solving ODES In case you haven't realized, there are a lot of methods for solving ODEs, with various properties. This homework set asks you to analyze one of them to determine its order of accuracy and stability characteristics. Here's the method: : def unknownMethod(f,yo,t): npts = t. shape [0] y = np.zeros((npts, yo.shape[0])) y[0] = yo for i in range(0, npts-1): h = t[i+1]-t[i] k1 = f(y[i],t[i]) k2 = f(y[i]+2.0*h*k1/3.0,t[i]+2.0*h/3.0) y[i+1] = y[i] + h*(0.25*k1 + 0.75*2) return y This method is one of a class of very commonly-used ODE solvers called Runge-Kutta methods. question 1 Define a function describing the system of ordinary differential equations dx =U dt du k X m dt With klm = 1 s-2 (1.e. the mass-spring oscillator described in lecture) : def spring(y, t): x = y[0] V = y[1] k = m = 1 return array([v,(-k/m)*x]) question 2 Test unknownMethod for 100 s with initial conditions x = 1, 0 = 0 and step size 0.1, and plot your result. t = arange(0, 100 ,.1) y = unknownMethod(spring, array([1,0]),t) plot(t,y[:,0],t,y[:,1]) legend('x', 'v'), loc = "upper left") xlabel('time') 14]: Text(0.5, 0, 'time') 1.00 0.75 0.50 0.25 0.00 -0.25 -0.50 -0.75 -1.00 40 80 100 time question 3 Write a function that finds the maximum absolute error between the unknownMethod solution and the known solution ( cos(t)) for the conditions in question 2 (100 s of solution, initial conditions x = 1, v= 0, but with the given step size) question 4 By using your function defined in question 3, determine the overall order of accuracy of unknownMethod. (in the block below, make the necessary computations and leave your answer and a brief explanation as a comment tag.) question 5 For a step size of 0.001 and the conditions above (100 s, etc.), make a plot of the error in the unknownMethod solution as a function of time