Question: Python. Please help me with just the two functions pr_fug and Pvap. The last two images are the inputs and solution you should get. Thanks
Python. Please help me with just the two functions pr_fug and Pvap. The last two images are the inputs and solution you should get. Thanks
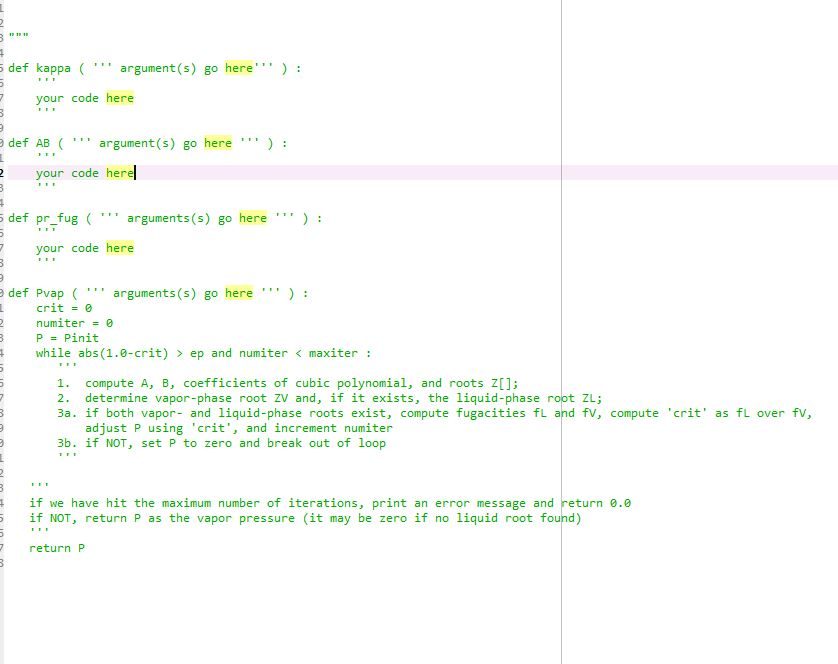





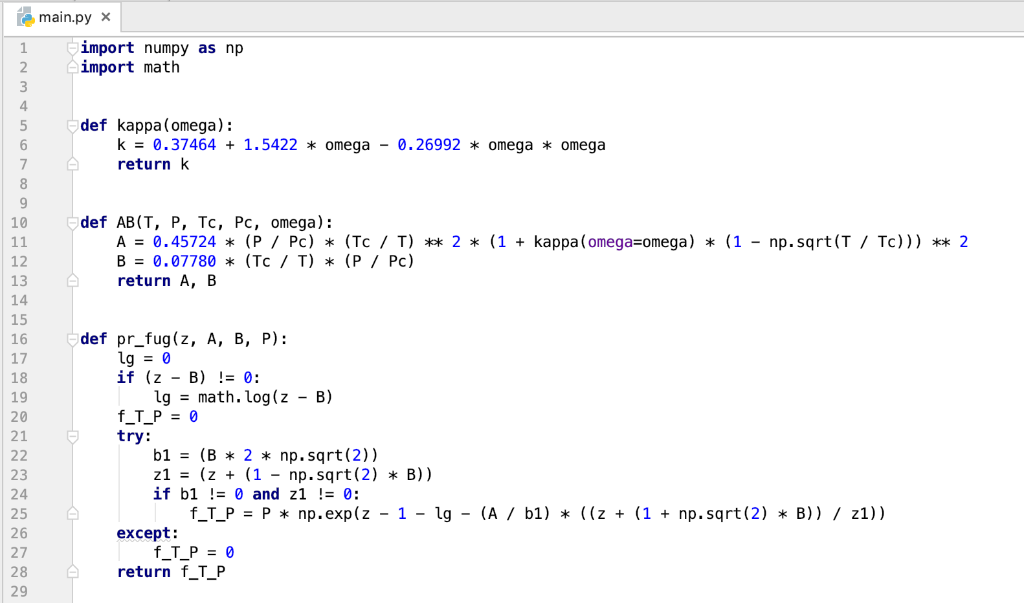
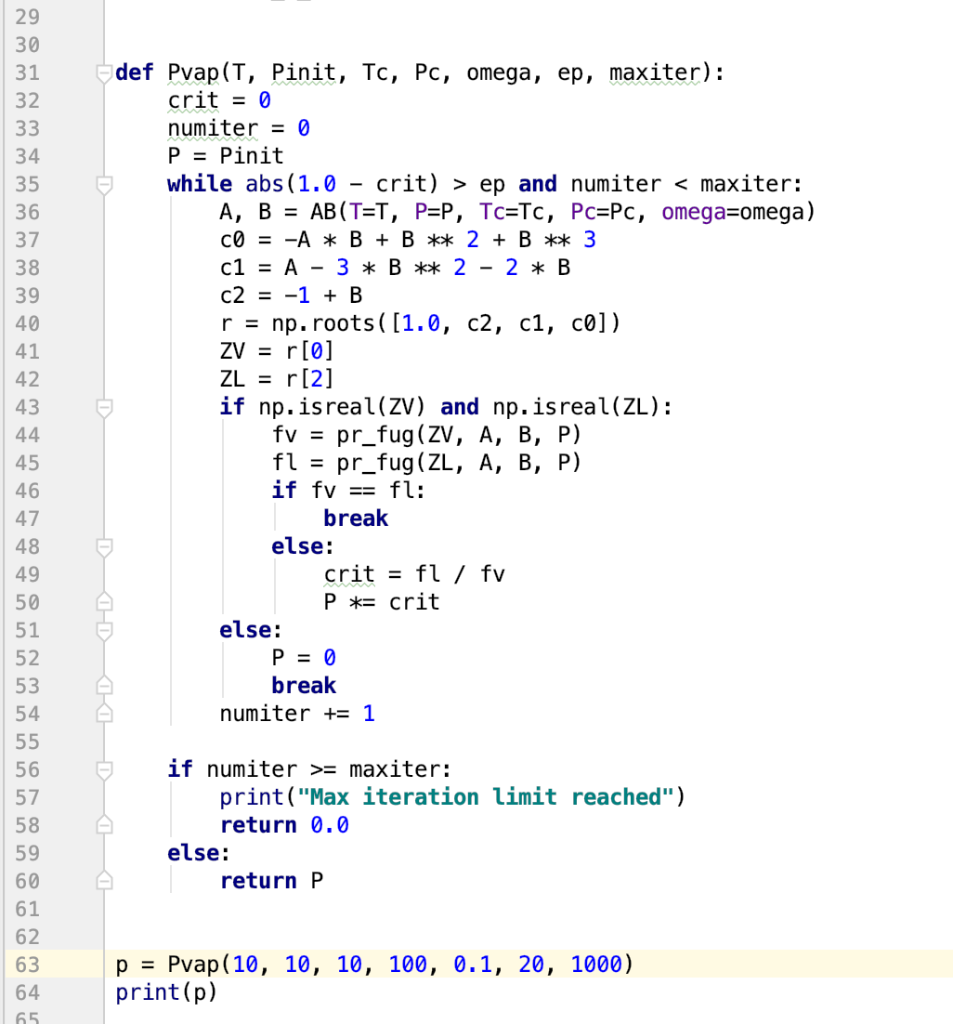
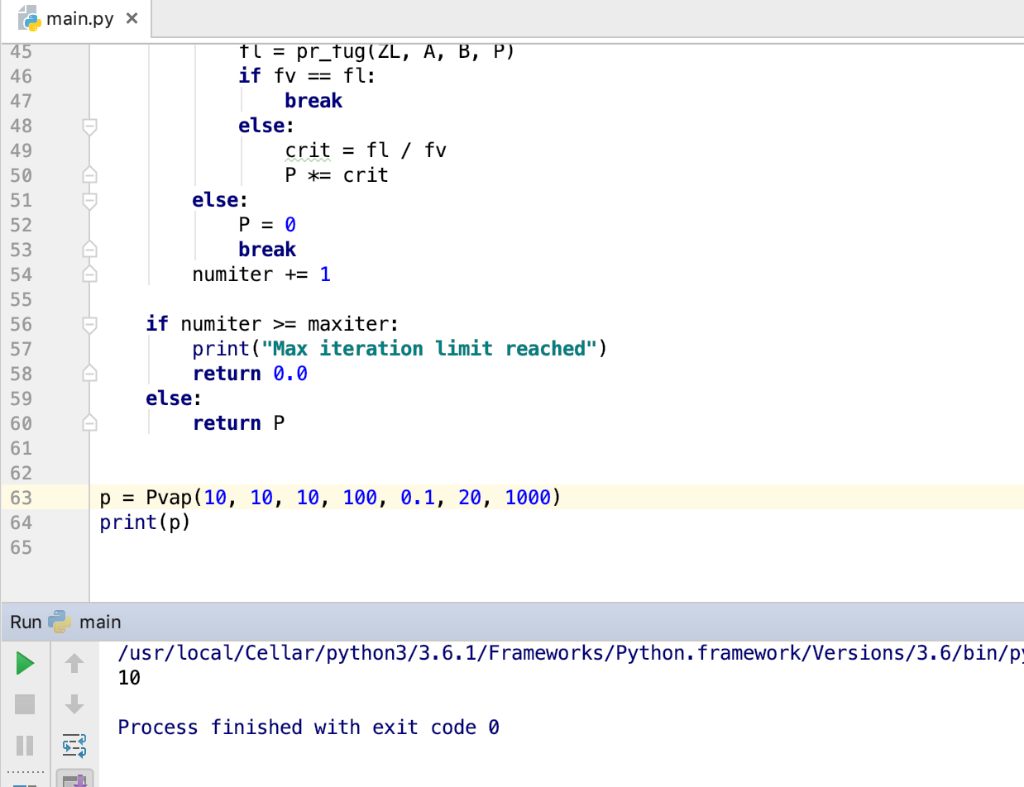
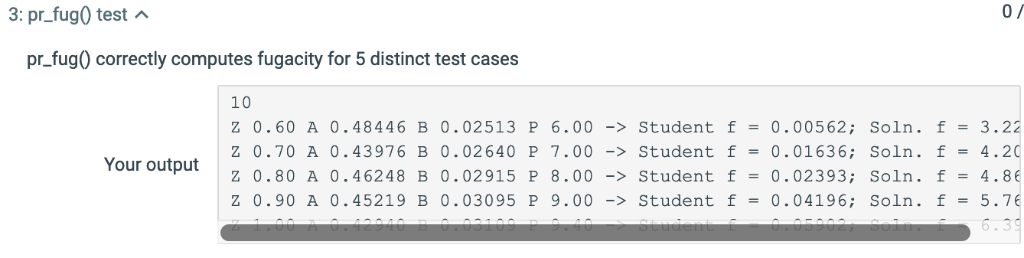
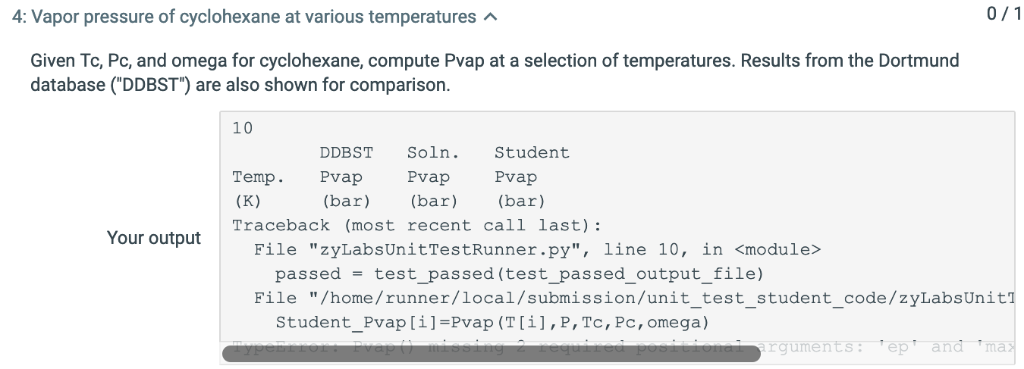
Assignment Using an IDE or text editor on your own computer, download and edit the template main.py to completely implement the following four functions: 1. kappa (omega): Returns the value of given the value of 2. AB (T,P, TC,Pc, omega): Returns both the values of PR parameters A and B given temperature T, pressure P, critical temperature To 3. pr_fug(Z,A,B,P) Computes the fugacity (in whatever units P has) given the value for Z (compressibility factor), A and B (the P-R 4. Pvap(T,Pinit,Tc,Pc, omega,ep,maxiter) Returns the vapor pressure pvap at temperature T for the pure substance with critical critical pressure Po, and acentricity factor w. parameters), and the pressure P (see eqn. 2) constants To P, and w;Pinit is an initial guess for the vapor pressure. ep is an optional argument with default value 1.e-6 that sets the tolerance for when two floating point numbers are equal. maxiter is an optional argument with default value 1,000 that sets the maximum number of iterations in the above algorithm. Pvap () will call the functions pr_fug() and AB(). and AB() will call kappa) def kappa ( argument(s) go here) your code here def AB argument (s) go here your code herel def pr_fug arguments (s) go here your code here def Pvaparguments (s) go here: crit = 0 numiter0 4while abs(1.0-crit) > ep and numiterfrom numpy import roots # return an array of -1, 1 a3 the roots to x^2-1 >roots (1, 0,-1]) # compute root of x^3-1 and store in array r >>r roots 1,0,0,-1) >print (r[01) (-0.5+0.866025403784)) >> print (z[i1) (0.5-0.866025403784) > print(r[i.real) >> print (r [11.imag) -0.86602540784 >print (r [21) # compute root3 f x^3-6 x^2 + 11 x - 6 = (x-3) (x-2) (x-1); note order of element 3 in array r >>r roots [1,-6,11, 6]) >print (r[01) >> print (z[11) >print (r [21) Notice that the character j is Python's default for the imaginary number sr(1), and complex numbers of tuples where the first element is the real part and the second is the imaginary part. One can access either part using the .real and imag methods 29 30 31 32 def Pvap(T, Pinit, Tc, Pc, omega, ep, maxiter): numiter0 P-Pinit while abs(1.0 crit) > ep and numiter 34 35 36 37 38 39 40 41 42 43 maxiter: omega-omega) A, B AB(T=T, P=P, Tc=Tc, Pc-PC, = r - np.roots ([1.0, c2, c1, c0]) if np.isreal (ZV) and np.isreal(ZL): fl-pr_fug(ZL, A, B, P) if fvfl: 45 46 47 48 49 50 51 break else: crit = fl / fv P *= crit else: 52 53 54 break numiter + 1 if numiter >- maxiter: 56 57 58 print("Max iteration limit reached") return 0.0 else: 59 60 61 62 63 64 65 return P pPvap (10, 10, 10, 100, 0.1, 20, 1000) print(p) main.py X A, B, P) t1 = pr-tug ( ZL, if fv fl: 46 47 48 49 50 51 52 53 54 break else: crit = fl / fv P crit else: break numiter + 1 if numiter >= maxiter: 56 57 58 59 60 61 62 63 64 65 print ("Max return 0.0 iteration limit reached") else: return P pPvap (10, 10, 10, 100, 0.1, 20, 1000) print(p) Runmain /usr/local/Cellar/python3/3.6.1/Frameworks/Python. framework/Versions/3.6/bin/p 10 Process finished with exit code 0 3: pr fug0 test pr fug0 correctly computes fugacity for 5 distinct test cases 10 0.60 A 0.48446 B 0.02513 P 6.00-> Student f = 0.00562; Soin. f = 3.22 Z 0.70 A 0.43976 B 0.02640 P 7.00-> Student f -0.01636; Soln. f 4.20 Z 0.80 A 0.46248 B 0.02915 P 8.00-> Student f = 0.02393; soln. f = 4.86 Z 0.90 A 0.45219 B 0.03095 P 9.00-> Student f 0.04196; Soln. f- 5.76 Your output : Vapor pressure of cyclohexane at various temperaturesA Given Tc, Pc, and omega for cyclohexane, compute Pvap at a selection of temperatures. Results from the Dortmund database ( DDBST) are also shown for comparison. 10 DDBST Soln. Student Temp. Pvap Pvap Pvap (bar (bar (bar) Traceback (most recent call last) Your output File "zyLabsUnitTestRunner.py", line 10, in
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


