Python please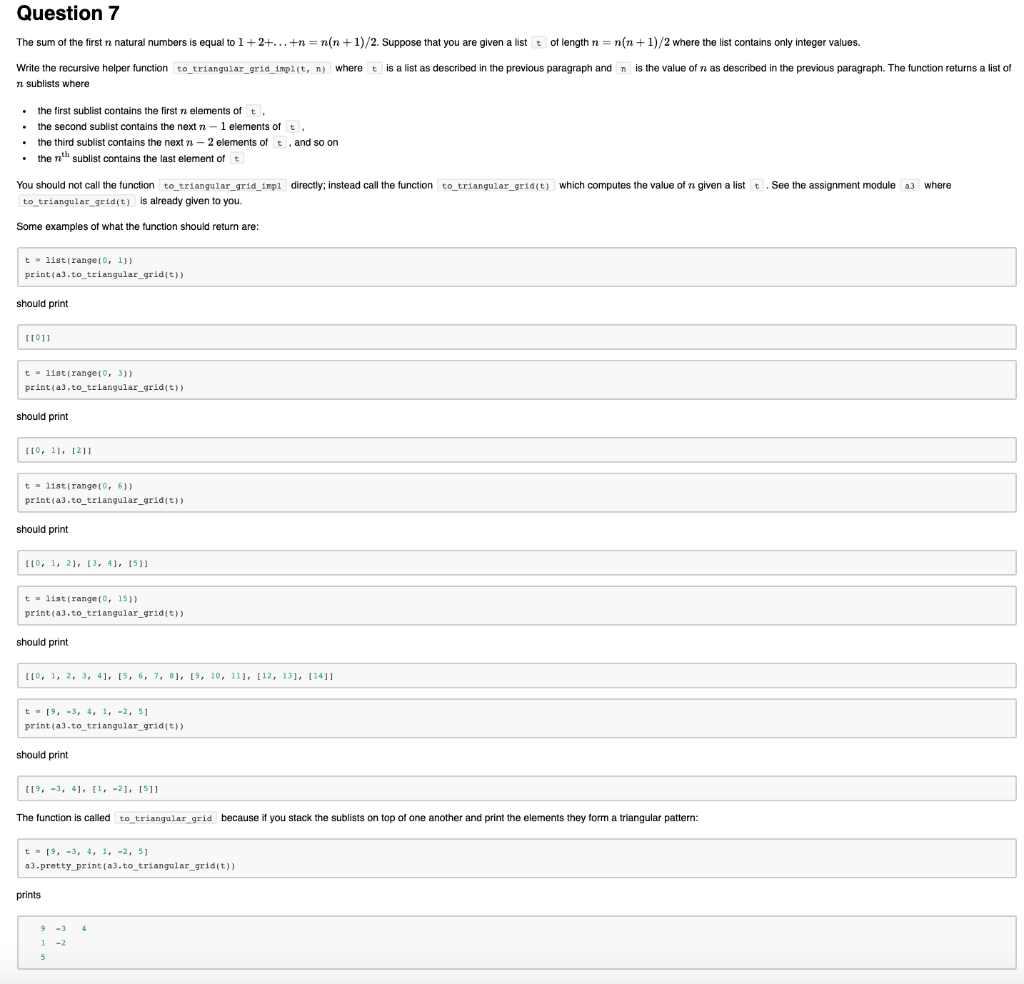

Question 7 The sum of the first n natural numbers is equal to 1+2+...+n=n(n+1)/2. Suppose that you are given a list t of length n= n(n+1)/2 where the list contains only integer values. Write the recursive helper function to_triangular_grid_impl(t, n) where t is a list as described in the previous paragraph and is the value of n as described in the previous paragraph. The function returns a list of 7 sublists where the first sublist contains the first n elements of t, the second sublist contains the next n - 1 elements of t. the third sublist contains the next n - 2 elements of t, and so on the nth sublist contains the last element of You should not call the function to triangular_grid_impl directly; instead call the function to_triangular_gridt) which computes the value of n given a list t . See the assignment module a3 where to triangular_grid(t) is already given to you. Some examples of what the function should return are: t-list (range(0, 1)) print(a3.to_triangular_grid/t)) should print 1011 t - list (range(0, 3)) print(a3.to_triangular_gridt)) should print 110, 11, 1211 t = list (range(0, 6)) print(a3.to_triangular_grid(t)) should print [[0, 1, 2], [3, 4], [5] t = list (range(0, 15)) print(a3.to_triangular_gridt) should print [[0, 1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11], [12, 13], [14]] t - [9, -3, 4, 1, -2, 5] print(a3.to triangular_gridt)) should print [[9, -3, 4]. [1, -2], [5]1 The function is called to_triangular grid because if you stack the sublists on top of one another and print the elements they form a triangular pattern: t - 19, -3,4,1, -2, 51 a3.pretty_print(a3.to_triangular_grid(t)) prints