python

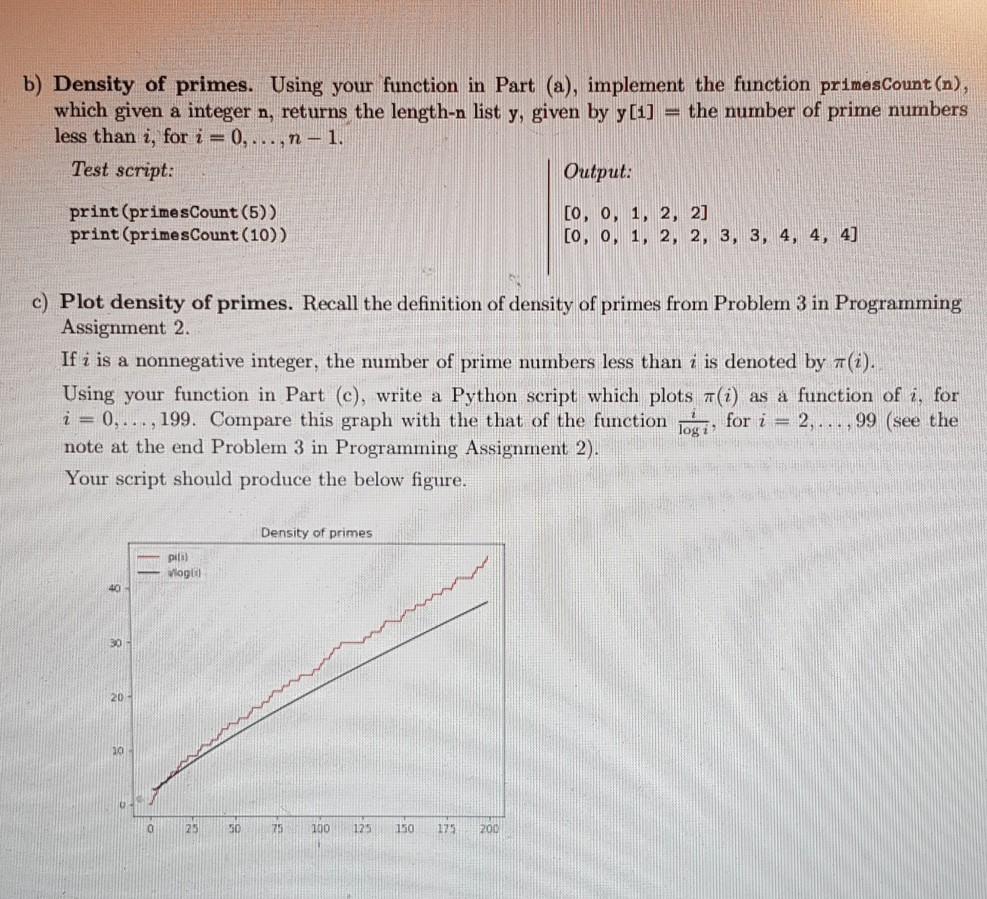
Problem 3. Primes revisited: generating primes, plotting density of prime a) Generate primes. Implement the function generatePrimes(n), which given a integer n, returns the tuple (P,B), where - P is a list consisitng of all prime number less than n, - B is a length-n boolean list given by: for i = 0,...,n-1, B[1]-True if i is prime and B[1]=False otherwise. Note that even though 0 and 1 are not promes, we are including i = 0,1 for convinience as indexing in lists starts from 0. We can solve this problem as in Problem 4.b in Programming Assignment 2: loop on i = 2, ..., 1-1, and for each i check if it is prime as in Problem4.a in Programming Assignment 2. In total, this algorithm takes O(nn) = 0(13/2) arithmetic operations. In this problem, you will use lists to do it more efficiently as done by the Ancient Greek scientist Eratosthenes around 200 BC. The idea of Eratosthenes is to write down the integers 2, 3, 4,...,n-1. Then cross all multiple all multiples of 2 less than n, then all multiples of 3 less than n, then move the next uncrossed number (i.e., 5) and cross all its multiples which are less than n, and so on. At some point there will be no next uncrossed number, in which case we stop. The uncrossed numbers are the prime numbers. Check the following wikipedia animation: https://en.wikipedia.org/wiki/File:Sieve_of_Eratosthenes_animation.gif Note that the above animation shows that the primes are being displayed as the numbers are being crossed (colored). You are not asked to do that. Instead, append them to the list P, initalized to the empty list 0. In this problem you are allowed to use the list.append method. Test program: Output: (P,B)-generatePrimes(2) O print (P) [2, 3, 5, 7] (P,B)-generatePrimes (10) [2, 3, 5, 7, 11, 13, 17, 19) print (P) [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, (PB)-generatePrimes (20) 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, print (P) 79, 83, 89, 97] (P,B)-generatePrimes (100) print (P) # Note: B will be used in Part (b) below It can be shown that it takes one log log n) arithmetic operations, which is significantly faster than O(123/2). Namely, up to a constant factor, it takes in the order of N = 1 + $ + 5 + + + arithmetic operations, where y is the largest prime less than n. It can be shown that N = O(n log log n) (this is beyond the scope of this course.) b) Density of primes. Using your function in Part (a), implement the function primesCount(n), which given a integer n, returns the length-n list y, given by y[1] = the number of prime numbers less than i, for i=0,...,n - 1. Output: Test script: print (primesCount(5)) print (primesCount(10)) [0, 0, 1, 2, 2] [0, 0, 1, 2, 2, 3, 3, 4, 4, 4] c) Plot density of primes. Recall the definition of density of primes from Problem 3 in Programming Assignment 2 If i is a nonnegative integer, the number of prime numbers less than i is denoted by 7(i). Using your function in Part (c), write a Python script which plots a(i) as a function of i, for i = 0... . , 199. Compare this graph with the that of the function logi, for i = 2,...,99 (see the note at the end Problem 3 in Programming Assignment 2). Your script should produce the below figure. Density of primes pital Viogli 40 30 20 25 50 75 100 125 150 175 200