Python Problem

Starting Code:

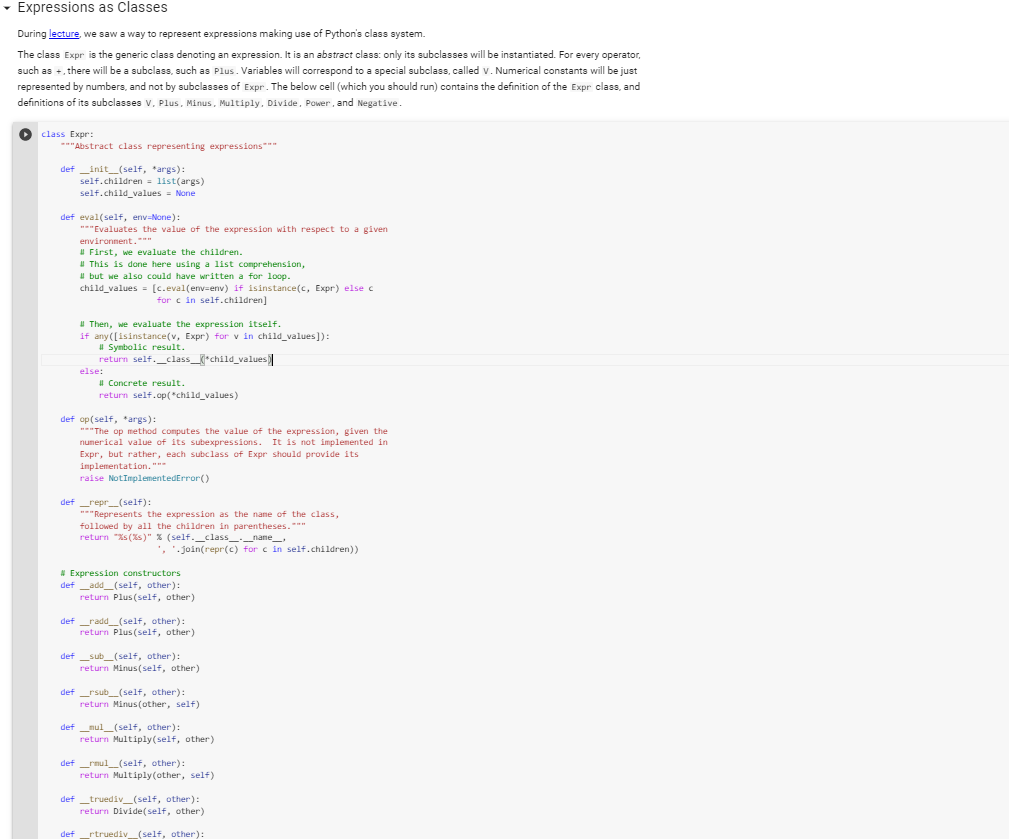
class Expr:

"""Abstract class representing expressions"""

def __init__(self, *args):

self.children = list(args)

self.child_values = None

def eval(self, env=None):

"""Evaluates the value of the expression with respect to a given

environment."""

# First, we evaluate the children.

# This is done here using a list comprehension,

# but we also could have written a for loop.

child_values = [c.eval(env=env) if isinstance(c, Expr) else c

for c in self.children]

# Then, we evaluate the expression itself.

if any([isinstance(v, Expr) for v in child_values]):

# Symbolic result.

return self.__class__(*child_values)

else:

# Concrete result.

return self.op(*child_values)

def op(self, *args):

"""The op method computes the value of the expression, given the

numerical value of its subexpressions. It is not implemented in

Expr, but rather, each subclass of Expr should provide its

implementation."""

raise NotImplementedError()

def __repr__(self):

"""Represents the expression as the name of the class,

followed by all the children in parentheses."""

return "%s(%s)" % (self.__class__.__name__,

', '.join(repr(c) for c in self.children))

# Expression constructors

def __add__(self, other):

return Plus(self, other)

def __radd__(self, other):

return Plus(self, other)

def __sub__(self, other):

return Minus(self, other)

def __rsub__(self, other):

return Minus(other, self)

def __mul__(self, other):

return Multiply(self, other)

def __rmul__(self, other):

return Multiply(other, self)

def __truediv__(self, other):

return Divide(self, other)

def __rtruediv__(self, other):

return Divide(other, self)

def __pow__(self, other):

return Power(self, other)

def __rpow__(self, other):

return Power(other, self)

def __neg__(self):

return Negative(self)

class V(Expr):

"""Variable."""

def __init__(self, *args):

"""Variables must be of type string."""

assert len(args) == 1

assert isinstance(args[0], str)

super().__init__(*args)

def eval(self, env=None):

"""If the variable is in the environment, returns the

value of the variable; otherwise, returns the expression."""

if env is not None and self.children[0] in env:

return env[self.children[0]]

else:

return self

class Plus(Expr):

def op(self, x, y):

return x + y

class Minus(Expr):

def op(self, x, y):

return x - y

class Multiply(Expr):

def op(self, x, y):

return x * y

class Divide(Expr):

def op(self, x, y):

return x / y

class Power(Expr):

def op(self, x, y):

return x ** y

class Negative(Expr):

def op(self, x):

return -x

Problem:

Test:

try:

from nose.tools import assert_equal, assert_almost_equal

from nose.tools import assert_true, assert_false

from nose.tools import assert_not_equal, assert_greater_equal

except:

!pip install nose

from nose.tools import assert_equal, assert_almost_equal

from nose.tools import assert_true, assert_false

from nose.tools import assert_not_equal, assert_greater_equal

Expressions as Classes During lecture, we saw a way to represent expressions making use of Python's class system. The class Expr is the generic class denoting an expression. It is an abstract class: only its subclasses will be instantiated. For every operator, such as there will be a subclass, such as Plus. Variables will correspond to a special subclass, called v. Numerical constants will be just represented by numbers, and not by subclasses of Expr. The below cell (which you should run) contains the definition of the Expr class, and definitions of its subclasses V, Plus, Minus, Multiply. Divide, Power, and Negative. class Expr: **Abstract class representing expressions def __init__(self, *args): self.children = list(args) self.child_values = None def eval(self, env=None): ** Evaluates the value of the expression with respect to a given environment." First, we evaluate the children. This is done here using a list comprehension, but we also could have written a for loop. child_values = [c.eval(env=env) if isinstance(C, Expr) else C for c in self.children] Then, we evaluate the expression itself. if any([isinstance(v, Expr) for v in child_values]): # Symbolic result. return self._class_ child_values else: # Concrete result. return self.op('child_values) def op(self, *args): "The op method computes the value of the expression, given the numerical value of its subexpressions. It is not implemented in Expr, but rather, each subclass of Expr should provide its implementation." raise NotImplementedError() def __repr_(self): "Represents the expression as the name of the class, followed by all the children in parentheses." return "X(S)" % (self._class_-_name__ ', '.join(repr(c) for c in self.children)) # Expression constructors def _add_(self, other): return Plus(self, other) def _radd__(self, other): return Plus(self, other) def _sub_(self, other): return Minus (self, other) def _rsub__(self, other): return Minus (other, self) def __mul_(self, other): return Multiply(self, other) def _rmul_(self, other): return Multiply(other, self) def _truediv_(self, other): return Divide(self, other) def rtruediv_(self, other): # Expression constructors def _add_(self, other): return Plus (self, other) def _radd__(self, other): return Plus(self, other) def _sub_(self, other): return Minus(self, other) def _rsub__(self, other): return Minus (other, self) def __mul_(self, other): return Multiply(self, other) def _rmul__(self, other): return Multiply(other, self) def _truediv_(self, other): return Divide(self, other) def _rtruediv_(self, other): return Divide (other, self) def _pow_(self, other): return Power(self, other) def _rpow__(self, other): return Power(other, self) def __neg_(self): return Negative(self) class V(Expr): ***Variable." def __init__(self, *args): Variables must be of type string." assert len(args) == 1 assert isinstance(args[@], str) super() __init_(*args) def eval(self, env=None): "If the variable is in the environment, returns the value of the variable; otherwise, returns the expression." if en is not None and self.children[@] in env: return env[self.children[@]] else: return self class Plus (Expr): def op(self, x, y): return x + y class Minus (Expr): def op(self, x, y): return x-Y class Multiply(Expr): def op(self, x, y): return x*y class Divide (Expr): def op(self, x, y): return x/y class Power (Expr): def op(self, x, y): return x ** y class Negative (Expr): def op (self, x): return - We have not yet implemented a way to take derivatives of Power expressions, that is, expressions involving exponentiation. As we saw during lecture, here's the definition of the derivative of an expression f9 with respect to 2: a 19 of e pe Tu 92 for + te log los 5). 2 To translate this into code, we need Logarithm to be one of our operators. Without it, the set of symbolic expressions would not be closed with respect to symbolic differentiation. We'd better add Logarithm to our collection of operators, and define a way to take the derivative of Logarithm expressions, too. Using de og f = 1 we define Logarithm to be a subclass of Expr, with op and op derivative methods, as seen during lecture: [] import math class Logarithm (Expr): def op(self, x): return math.log(x) def op_derivative (self, var, partials): return Multiply Divide(1, self.children[@]), partials[0] Now we have everything we need to take derivatives of Power expressions. For this problem, you will implement the op_derivative method for the power class, making use of Logarithm. [ ] def power_op_derivative(self, var, partials): "Implements derivative for Divide expressions. Should take no more than 5 lines of code to write."" # YOUR CODE HERE raise Not ImplementedError() Power.op_derivative = power_op_derivative [ ] ### Tests for Power.op_derivative ## We test your code by taking the derivative of expressions involving exponentiation, ## then evaluating the resulting expression for particular values of the variables # The derivative of x**2 with respect to x is 2x, which is equal to 6 when x = 3 e = V('x') ** 2 assert_almost_equal(e.derivative('x').eval(dict(x=3)), 6) # The derivative of x**2 with respect to y is o e = V('x') ** 2 assert_almost_equal(e.derivative('y').eval(dict(x=3)), ) [] ### More tests for 'Power.op_derivative e = 3 ** V('x') assert_almost_equal(e.derivative('x').eval(dict(x=4)), math.log(3) * (3 ** 4), places=2) e = V('x') ** 2.8 assert_almost_equal(e. derivative('x').eval(dict(x=3)), 2.8 * 3 ** 1.8, places-2) Expressions as Classes During lecture, we saw a way to represent expressions making use of Python's class system. The class Expr is the generic class denoting an expression. It is an abstract class: only its subclasses will be instantiated. For every operator, such as there will be a subclass, such as Plus. Variables will correspond to a special subclass, called v. Numerical constants will be just represented by numbers, and not by subclasses of Expr. The below cell (which you should run) contains the definition of the Expr class, and definitions of its subclasses V, Plus, Minus, Multiply. Divide, Power, and Negative. class Expr: **Abstract class representing expressions def __init__(self, *args): self.children = list(args) self.child_values = None def eval(self, env=None): ** Evaluates the value of the expression with respect to a given environment." First, we evaluate the children. This is done here using a list comprehension, but we also could have written a for loop. child_values = [c.eval(env=env) if isinstance(C, Expr) else C for c in self.children] Then, we evaluate the expression itself. if any([isinstance(v, Expr) for v in child_values]): # Symbolic result. return self._class_ child_values else: # Concrete result. return self.op('child_values) def op(self, *args): "The op method computes the value of the expression, given the numerical value of its subexpressions. It is not implemented in Expr, but rather, each subclass of Expr should provide its implementation." raise NotImplementedError() def __repr_(self): "Represents the expression as the name of the class, followed by all the children in parentheses." return "X(S)" % (self._class_-_name__ ', '.join(repr(c) for c in self.children)) # Expression constructors def _add_(self, other): return Plus(self, other) def _radd__(self, other): return Plus(self, other) def _sub_(self, other): return Minus (self, other) def _rsub__(self, other): return Minus (other, self) def __mul_(self, other): return Multiply(self, other) def _rmul_(self, other): return Multiply(other, self) def _truediv_(self, other): return Divide(self, other) def rtruediv_(self, other): # Expression constructors def _add_(self, other): return Plus (self, other) def _radd__(self, other): return Plus(self, other) def _sub_(self, other): return Minus(self, other) def _rsub__(self, other): return Minus (other, self) def __mul_(self, other): return Multiply(self, other) def _rmul__(self, other): return Multiply(other, self) def _truediv_(self, other): return Divide(self, other) def _rtruediv_(self, other): return Divide (other, self) def _pow_(self, other): return Power(self, other) def _rpow__(self, other): return Power(other, self) def __neg_(self): return Negative(self) class V(Expr): ***Variable." def __init__(self, *args): Variables must be of type string." assert len(args) == 1 assert isinstance(args[@], str) super() __init_(*args) def eval(self, env=None): "If the variable is in the environment, returns the value of the variable; otherwise, returns the expression." if en is not None and self.children[@] in env: return env[self.children[@]] else: return self class Plus (Expr): def op(self, x, y): return x + y class Minus (Expr): def op(self, x, y): return x-Y class Multiply(Expr): def op(self, x, y): return x*y class Divide (Expr): def op(self, x, y): return x/y class Power (Expr): def op(self, x, y): return x ** y class Negative (Expr): def op (self, x): return - We have not yet implemented a way to take derivatives of Power expressions, that is, expressions involving exponentiation. As we saw during lecture, here's the definition of the derivative of an expression f9 with respect to 2: a 19 of e pe Tu 92 for + te log los 5). 2 To translate this into code, we need Logarithm to be one of our operators. Without it, the set of symbolic expressions would not be closed with respect to symbolic differentiation. We'd better add Logarithm to our collection of operators, and define a way to take the derivative of Logarithm expressions, too. Using de og f = 1 we define Logarithm to be a subclass of Expr, with op and op derivative methods, as seen during lecture: [] import math class Logarithm (Expr): def op(self, x): return math.log(x) def op_derivative (self, var, partials): return Multiply Divide(1, self.children[@]), partials[0] Now we have everything we need to take derivatives of Power expressions. For this problem, you will implement the op_derivative method for the power class, making use of Logarithm. [ ] def power_op_derivative(self, var, partials): "Implements derivative for Divide expressions. Should take no more than 5 lines of code to write."" # YOUR CODE HERE raise Not ImplementedError() Power.op_derivative = power_op_derivative [ ] ### Tests for Power.op_derivative ## We test your code by taking the derivative of expressions involving exponentiation, ## then evaluating the resulting expression for particular values of the variables # The derivative of x**2 with respect to x is 2x, which is equal to 6 when x = 3 e = V('x') ** 2 assert_almost_equal(e.derivative('x').eval(dict(x=3)), 6) # The derivative of x**2 with respect to y is o e = V('x') ** 2 assert_almost_equal(e.derivative('y').eval(dict(x=3)), ) [] ### More tests for 'Power.op_derivative e = 3 ** V('x') assert_almost_equal(e.derivative('x').eval(dict(x=4)), math.log(3) * (3 ** 4), places=2) e = V('x') ** 2.8 assert_almost_equal(e. derivative('x').eval(dict(x=3)), 2.8 * 3 ** 1.8, places-2)