Python Program for c,d,f,h

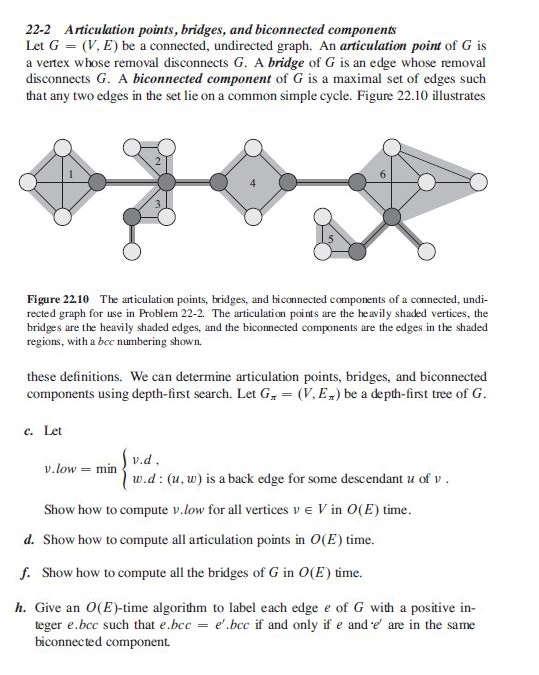
22-2 Articulation points, bridges, and biconnected components Let G - (V, E) be a connected, undirected graph. An articulation point of G is a ventex whose removal disconnects G. A bridge of G is an edge whose removal disconnects G. A biconnected component of G is a maximal set of edges such that any two edges in the set lie on a common simple cycle. Figure 22.10 illustrates Figure 2210 The articulation points, bridges, and biconnected components of a connected, undi rected graph for use in Problem 22-2. The articulation points are the heavily shaded vertices, the bridges are the heavily shaded cdges, and the biconnected components are the edges in the shaded regions, with a bee numbering shown. these definitions. We can determine articulation points, bridges, and biconnected components using depth-first search. Let G. = (V, EX) be a depth-first tree of G. C. Let w.d w.low , min w.d: (u , w) is a back edge for some descendant U of V. Show how to compute v.low for all vertices v E V in O(E) time. d. Show how to compute all articulation points in O(E) time. S. Show how to compute all the bridges of G in o(E) time. h. Give an o(E)-time algorithm to label each edge e of G with a positive in Leger e.bce such that e.bce = e .bce if and only if e and e are in the same biconnected component