python3

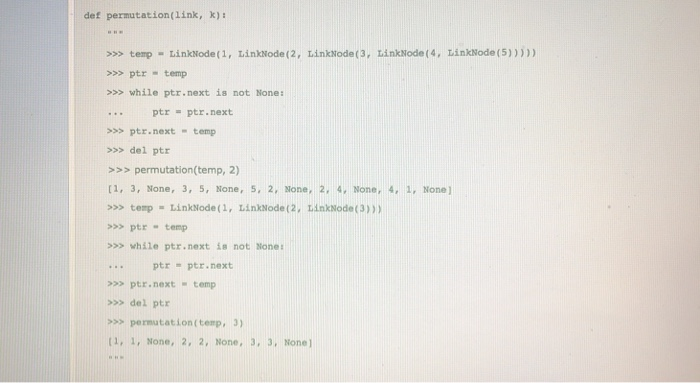
A permutation can be considered as an injective (one-to-one) mapping. For example, the permutation p (1,2,3,4,5) can be considered as a mapping p(x) from the set of integers [5] to set of integers [5], such that 1 maps to 2, 2 maps to 3, 3 maps to 4, 4 maps to 5, finally 5 maps back to 1. In this problem, we'll use circular singly linked-lists to represent this kind of permutation with one cycle. The circular singly linked-list representation of the previous example will look like: 2345 Now, we want to calculate p(x) raised to kth power, i.e. we want to apply the mapping p to itself k times. Say, if we have k-2, 3 4 5 4 5 2 The resulting would map 1 to 3, 3 to 5, 5 to 2, 2 to 4, then finally 4 maps back to 1, which closes the cycle. The permutation However, raising the permutation to kth power doesn't always result in one single nice closed cycle. For example, if you raise q- (1,2,3) to the 3rd power, you will end up 3 separate cycles (1 maps to 1, 2 maps to 2, 3 maps to 3). To make your life easier, we will always store the resulting mapping as a list of doublets for this problem, i.e. [1->3, 3->5, 5-2, 2- >4, 4.11 for the first example, and [1->1, 2->2, 3->3] for the second example, where each doublet is a linked-list object. Now that we have introduced the terms, write a function that takes a permutation with one cycle (represented as a circular-linked list) and a positive integer k, and returns the specified representation of raising the permutation to the kth power def permutation(link, k) ptr temp s while ptr.next is not None: ptr= ptr. next ptr.next-temp >>> del ptr >>>permutation(temp, 2) 1, 3, None, 3, 5, None, 5, 2, None, 2. 4, None, 4, 1, None >>> temp LinkNode ( 1 , LinkNode ( 2 , LinkNode ( 3 ) ) ptrtemp x while ptr.next is not None: ptr ptr.next ptr.nexttemp >> del ptr >>> permutation(temp, 3) [1, 1, None, 2, 2, None, 3, 3, None) A permutation can be considered as an injective (one-to-one) mapping. For example, the permutation p (1,2,3,4,5) can be considered as a mapping p(x) from the set of integers [5] to set of integers [5], such that 1 maps to 2, 2 maps to 3, 3 maps to 4, 4 maps to 5, finally 5 maps back to 1. In this problem, we'll use circular singly linked-lists to represent this kind of permutation with one cycle. The circular singly linked-list representation of the previous example will look like: 2345 Now, we want to calculate p(x) raised to kth power, i.e. we want to apply the mapping p to itself k times. Say, if we have k-2, 3 4 5 4 5 2 The resulting would map 1 to 3, 3 to 5, 5 to 2, 2 to 4, then finally 4 maps back to 1, which closes the cycle. The permutation However, raising the permutation to kth power doesn't always result in one single nice closed cycle. For example, if you raise q- (1,2,3) to the 3rd power, you will end up 3 separate cycles (1 maps to 1, 2 maps to 2, 3 maps to 3). To make your life easier, we will always store the resulting mapping as a list of doublets for this problem, i.e. [1->3, 3->5, 5-2, 2- >4, 4.11 for the first example, and [1->1, 2->2, 3->3] for the second example, where each doublet is a linked-list object. Now that we have introduced the terms, write a function that takes a permutation with one cycle (represented as a circular-linked list) and a positive integer k, and returns the specified representation of raising the permutation to the kth power def permutation(link, k) ptr temp s while ptr.next is not None: ptr= ptr. next ptr.next-temp >>> del ptr >>>permutation(temp, 2) 1, 3, None, 3, 5, None, 5, 2, None, 2. 4, None, 4, 1, None >>> temp LinkNode ( 1 , LinkNode ( 2 , LinkNode ( 3 ) ) ptrtemp x while ptr.next is not None: ptr ptr.next ptr.nexttemp >> del ptr >>> permutation(temp, 3) [1, 1, None, 2, 2, None, 3, 3, None)