Question: Q 1 Consider a 4 X 4 matrix A, which has four eigenvalues: A0 = 0, A1 : 11 A2 = 2, A3 : 3.

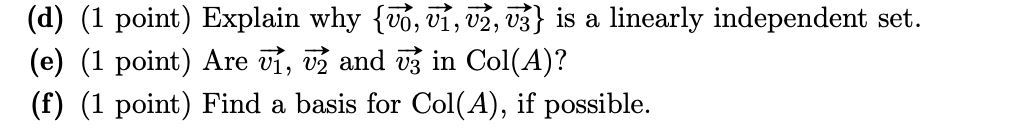
Q 1 Consider a 4 X 4 matrix A, which hasfour eigenvalues: A0 = 0, A1 : 11 A2 = 2, A3

Q 1 Consider a 4 X 4 matrix A, which has four eigenvalues: A0 = 0, A1 : 11 A2 = 2, A3 : 3. Assume that 136 is an eigenvector of A0, 171 is an eigenvector of A1, 113 is an eigenvector of A2 and 133' is an eigenvector of A3. (For each of the question parts, briey justify your answer and show your work step-by-step. Correct answers not supported by substantive explanations will receive no credit.) (d) (1 point) Explain why { vo, v1, v2, 13} is a linearly independent set. (e) (1 point) Are vi, v2 and v3 in Col(A)? (f) (1 point ) Find a basis for Col(A), if possible

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

Q 1 Consider a 3 x 3 matrix A, which has three eigenvalues, A0 = 0, A1 = 1, A2 = 2. Assume that 176 is an eigenvector of Ag, '61 is an eigenvector of A1 and IE is an eigenvector of A2. (For each of...

Q:

how do I approach this? Consider the following third order system * = Ax + Bu, x(t) ER, uER! Assume that the characteristic polynomial is given by p(1) = det ()I - A) = 13 + a2s' +ais + ao and...

Q:

1. Check all that apply. A. Since Ying's loop pointer, p , is type Base , no compiler error will occur. B. Ying can call p->func() on each object in the loop and get distinct behavior as defined by...

Q:

1. Check all that apply. A. Since Ying's loop pointer, p , is type Base , no compiler error will occur. B. Ying can call p->func() on each object in the loop and get distinct behavior as defined by...

Q:

[54pts] : Consider the 2 X 4 matrix _ U 0 2 U A 1 0 U 1 and let T = rank{A). We will work our way toward the Singular Value Decomposition (SVD) of A and to the pseudoinverse of A. a.) Briefly explain...

Q:

[54pts] : Consider the 2 X 4 matrix _ U 0 2 U A 1 0 U 1 and let T = rank{A). We will work our way toward the Singular Value Decomposition (SVD) of A and to the pseudoinverse of A. a.) Briefly explain...

Q:

Q 1 2 3 4 5 6 7 8 9 10 Answe r Q 11 1 21 31 41 51 61 71 81 92 0 Answe r Q Answe r 2 12 22 32 42 52 62 72 82 93 0 Q 3 13 23 33 43 53 63 73 83 94 0 1 Answe r Q 4 14 24 34 44 54 64 74 84 95 0 Answer Use...

Q:

1. Check all that apply. A. Since Ying's loop pointer, p , is type Base , no compiler error will occur. B. Ying can call p->func() on each object in the loop and get distinct behavior as defined by...

Q:

MBA624-MSF624 - Exam 1 - Spring 2017 MBA624-MSF624 (Fall 2017) - Exam 1 The test link will become visible in Assignments course area at 8:00 a.m. CST on Fri, Oct 13, 2017. Due date is: 8:00 a.m. CST...

Q:

MBA 610 - Exam 1 This is a take-home exam, containing 50 questions, each worth 2 points (total of 100 points). You may use your book, notes, calculator, Excel, and other resources such as videos and...

Q:

Andersons Armoires reported net loss for the year of $25,000; however, it reported an increase in cash balance of $50,000. The CFO states, Andersons Armoires would have shown a profit were it not for...

Q:

Geocentric Company purchased 1000 shares of Robust Company at $50 per share and incurred a brokerage fee of $100 on September 1, 2019. A. What entry would Geocentric make to record this purchase? B....

Q:

Current Attempt in Progress Sheridan Compary is considering investing in an anfilty contract that will retirn $ 3 0 0 0 0 amually at the end of each year for 1 9 years. tidineretovien the factor...

Q:

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...