Q 1a) Apply linear programming (LP) to formulate the problem to determine the number of computers the university should rent each month and for how long, so that the total cost of renting is minimum

1b) Solve the LP model in Question 1a by developing a spreadsheet model. How many computers should the university rent each month and for how long? What is the optimal cost of renting? You can assume that fractional rental is possible. Present your solutions by rounding up or down the number.

1c) How does the model change if the university has 50 computers at the start of the year? Is there any change in the solution obtained in Question 1a?

1d) If the university wants the solution only in integer numbers, what amendments need to be done to the previous model? Solve for the best solution in this case.

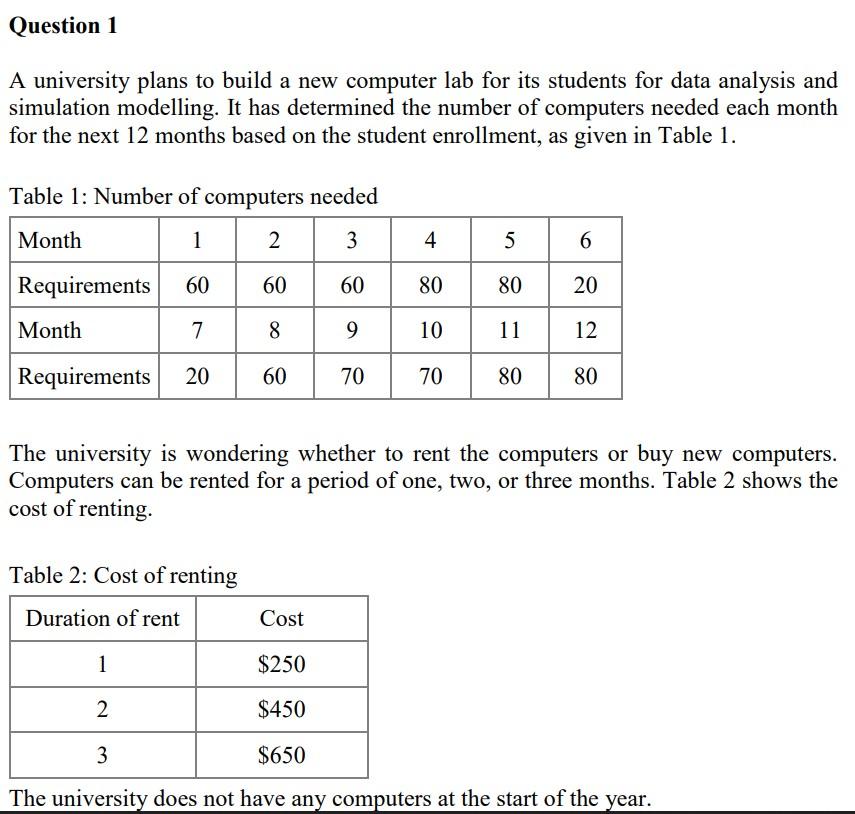
A university plans to build a new computer lab for its students for data analysis and simulation modelling. It has determined the number of computers needed each month for the next 12 months based on the student enrollment, as given in Table 1. Table 1: Number of computers needed The university is wondering whether to rent the computers or buy new computers. Computers can be rented for a period of one, two, or three months. Table 2 shows the cost of renting. Table 2: Cost of renting The university does not have any computers at the start of the year