Q$3$ k$-$Minimum Spanning Tree

Consider the so$-$called $k-$Minimum Spanning Tree $(k-$MST$)$ problem, which is defined as follows.

An instance of the $k-$MST problem is given by a connected undirected graph $G=(V,E)$ with

edge weights $w$:$EQ$ and a natural number $k>2.$ The question is to find a tree with exactly $k$

nodes that is a subgraph of $G$ and minimises the weight among all such trees. Informally, $k-$MST is

the variant of the minimum spanning tree problem, where instead of a spanning tree one wants to

find a tree with exactly $k$ nodes.

What would be the result if we apply Prim's, respectively Kruskal's, algorithm to the problem by

stopping both algorithms after $k-1$ edges have been added? In the following we refer to these

versions of Prim's and Kruskal's algorithm as the modified algorithm of Prime or Kruskal,

respectively.

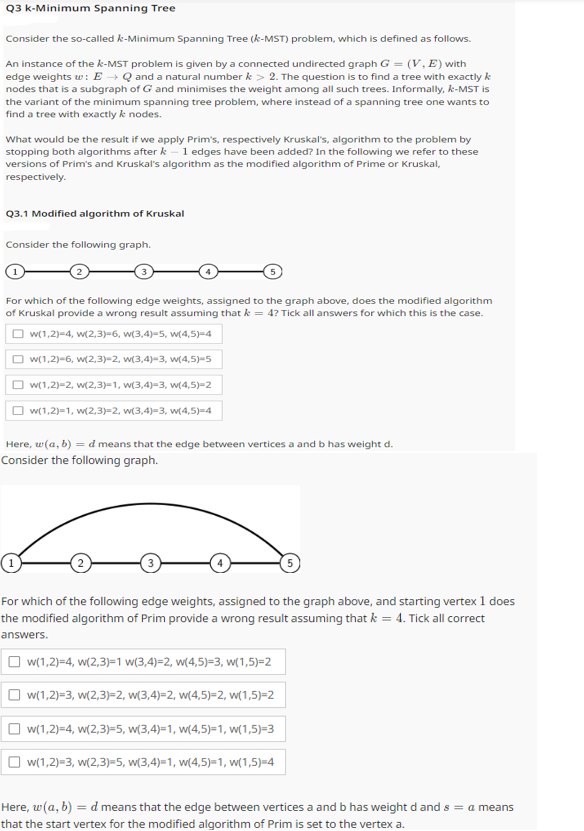
Q$3\mathrm{.}1$ Modified algorithm of Kruskal

Consider the following graph.

For which of the following edge weights, assigned to the graph above, does the modified algorithm

of Kruskal provide a wrong result assuming that $k=4?$ Tick all answers for which this is the case.

$w(1,2)=4,w(2,3)=6,w(3,4)=5,w(4,5)=4$

$w(1,2)=6,w(2,3)=2,w(3,4)=3,w(4,5)=5$

$w(1,2)=2,w(2,3)=1,w(3,4)=3,w(4,5)=2$

$w(1,2)=1,w(2,3)=2,w(3,4)=3,w(4,5)=4$

Here, $w(a,b)=d$ means that the edge between vertices a and $b$ has weight $d.$

Consider the following graph.

For which of the following edge weights, assigned to the graph above, and starting vertex $1$ does

the modified algorithm of Prim provide a wrong result assuming that $k=4.$ Tick all correct

answers.

$w(1,2)=4,w(2,3)=1w(3,4)=2,w(4,5)=3,w(1,5)=2$

$w(1,2)=3,w(2,3)=2,w(3,4)=2,w(4,5)=2,w(1,5)=2$

$w(1,2)=4,w(2,3)=5,w(3,4)=1,w(4,5)=1,w(1,5)=3$

$w(1,2)=3,w(2,3)=5,w(3,4)=1,w(4,5)=1,w(1,5)=4$

Here, $w(a,b)=d$ means that the edge between vertices a and $b$ has weight $d$ and $s=$a means

that the start vertex for the modified algorithm of Prim is set to the vertex a$.$