Q$3.$ Piping Networks $\backslash$& Systems $-$ Parallel Configuration:

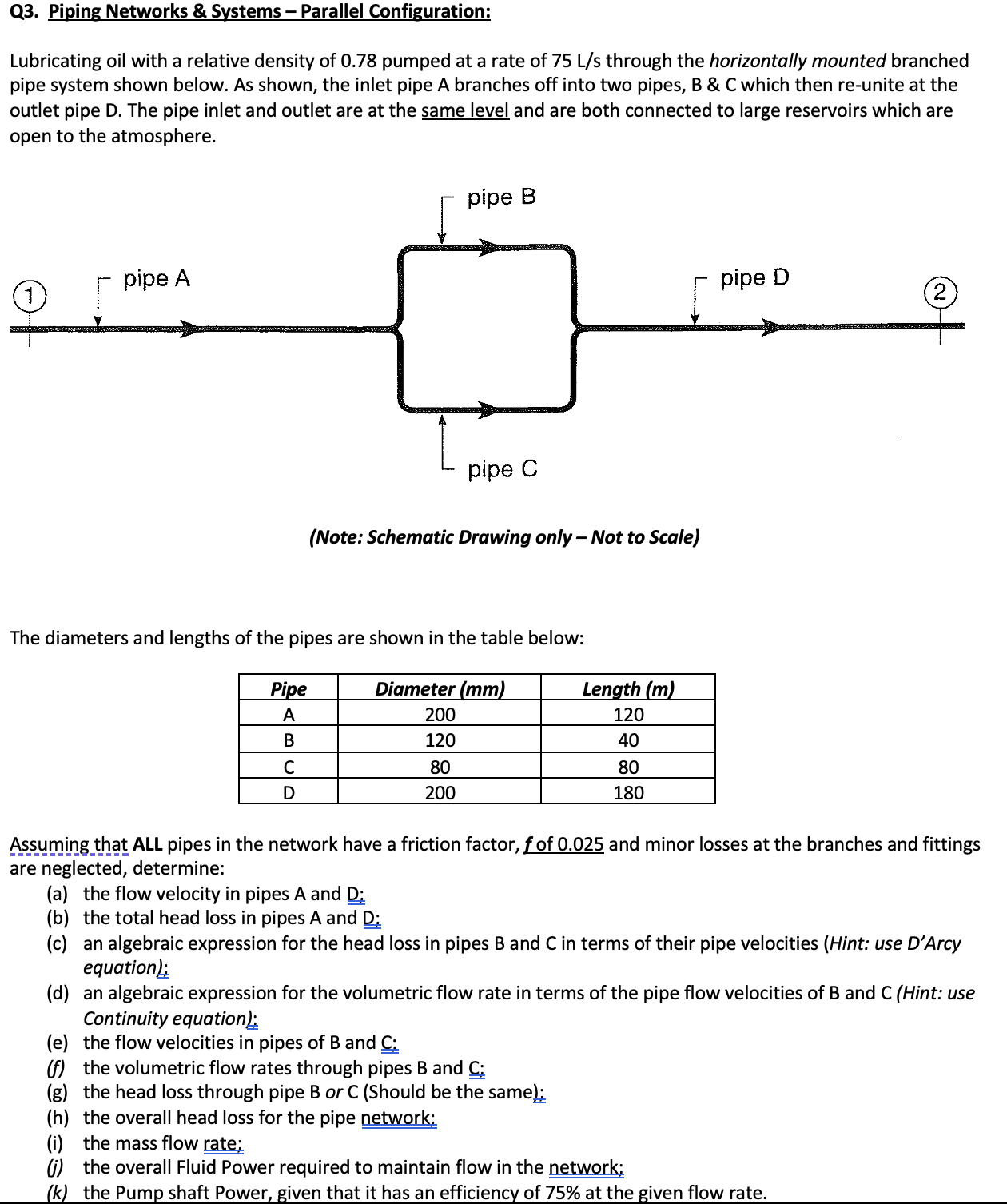
Lubricating oil with a relative density of $0\mathrm{.}78$ pumped at a rate of $\backslash (75\backslash$mathrm$\{$~L$\}/\backslash$mathrm$\{$s$\}\backslash )$ through the horizontally mounted branched pipe system shown below. As shown, the inlet pipe $\backslash ($ A $\backslash )$ branches off into two pipes, $\backslash ($ B $\backslash )\backslash$& $\backslash ($ C $\backslash )$ which then re$-$unite at the outlet pipe D$.$ The pipe inlet and outlet are at the same level and are both connected to large reservoirs which are open to the atmosphere.

$($Note: Schematic Drawing only $-$ Not to Scale$)$

The diameters and lengths of the pipes are shown in the table below:

$\backslash$begin$\{$tabular$\}\{|$c$|$c$|$c$|\}$

$\backslash$hline Pipe & Diameter $\backslash ((\backslash$mathbf$\{$m m$\})\backslash )$ & Length $\backslash ((\backslash$boldsymbol$\{$m$\})\backslash )\backslash \backslash$

$\backslash$hline A & $200$ & $120\backslash \backslash$

$\backslash$hline B & $120$ & $40\backslash \backslash$

$\backslash$hline C & $80$ & $80\backslash \backslash$

$\backslash$hline D & $200$ & $180\backslash \backslash$

$\backslash$hline

$\backslash$end$\{$tabular$\}$

Assuming that ALL pipes in the network have a friction factor, $\backslash ($ f $\backslash )$ of $0\mathrm{.}025$ and minor losses at the branches and fittings are neglected, determine:

$($a$)$ the flow velocity in pipes $\backslash ($ A $\backslash )$ and $\backslash (\backslash$underline$\{$D$\}\backslash )$;

$($b$)$ the total head loss in pipes $\backslash ($ A $\backslash )$ and $\backslash (\backslash$underline$\{$D$\}\_\{\backslash$text $\{$; $\}\}\backslash )$

$($c$)$ an algebraic expression for the head loss in pipes B and C in terms of their pipe velocities $($Hint: use D'Arcy equation$)$:

$($d$)$ an algebraic expression for the volumetric flow rate in terms of the pipe flow velocities of $\backslash ($ B $\backslash )$ and $\backslash ($ C $\backslash )($Hint: use Continuity equation$)$;

$($e$)$ the flow velocities in pipes of $\backslash ($ B $\backslash )$ and $\backslash (\backslash$underline$\{\backslash$underline$\{$C$\}\}\backslash )$;

$($f$)$ the volumetric flow rates through pipes B and C ;

$($g$)$ the head loss through pipe B or C $($Should be the same$)$;

$($h$)$ the overall head loss for the pipe network;

$($i$)$ the mass flow rate;

$($j$)$ the overall Fluid Power required to maintain flow in the network;

$($k$)$ the Pump shaft Power, given that it has an efficiency of $\backslash (75\backslash \%\backslash )$ at the given flow rate.