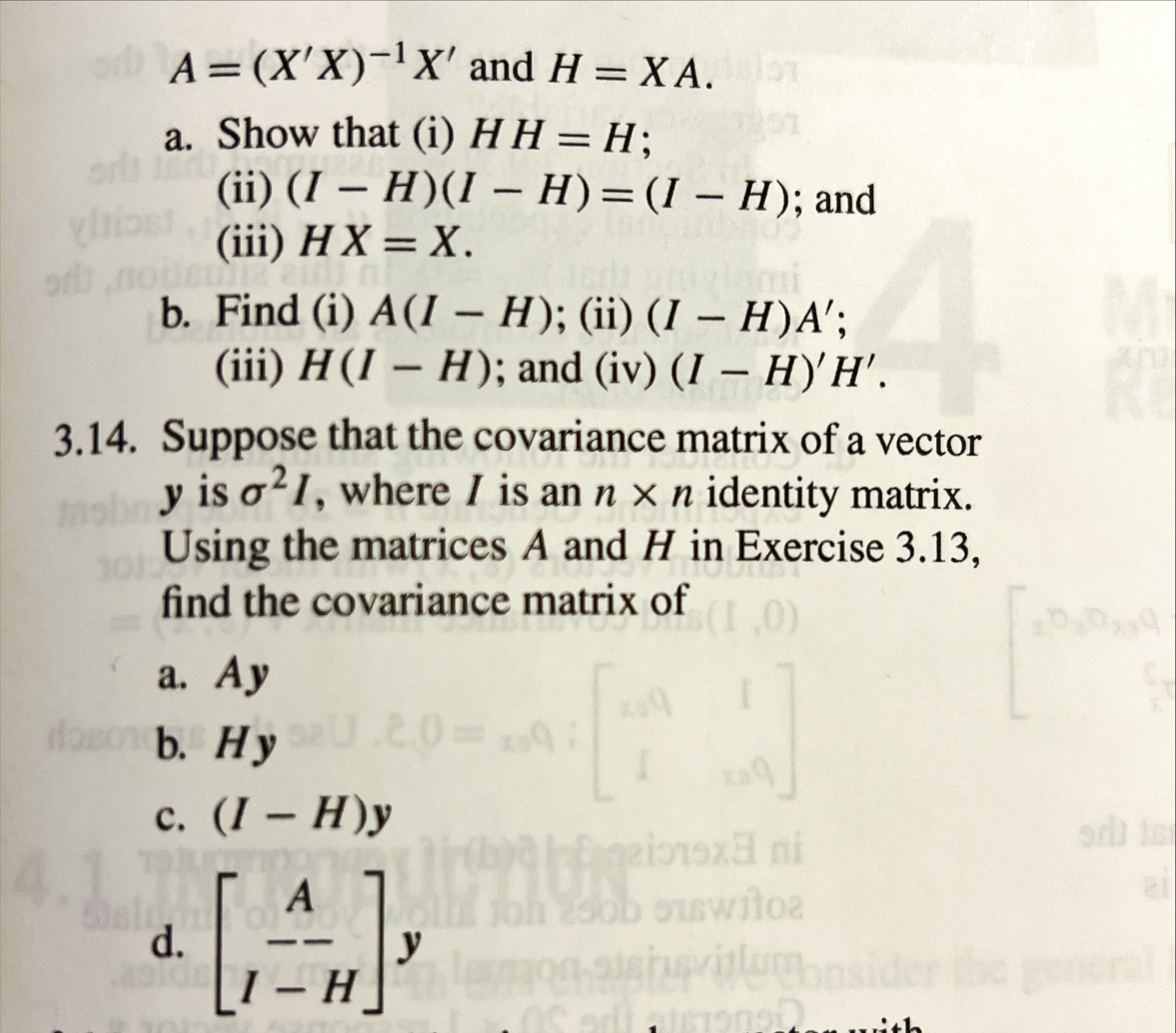
Q 3.13 Let X be an n x p matrix. Assume that the inverse (X' X)^-1 exists, and define A = (X' X)^-1 X' and H = XA.

a. Show that

(i) H H = H;

(ii) (I-H)(I-H) = (I-H); and

(iii) HX = X

b. Find (i) A(I-H); (ii) (I-H)A'; (iii) H(I-H); and (iv) (I-H)'H'

Q 3.14 please see the following picture.

Please use linear statistical model way to solve this problem. Please help solve both 3.13 and 3.14 questions. Thank you so much.

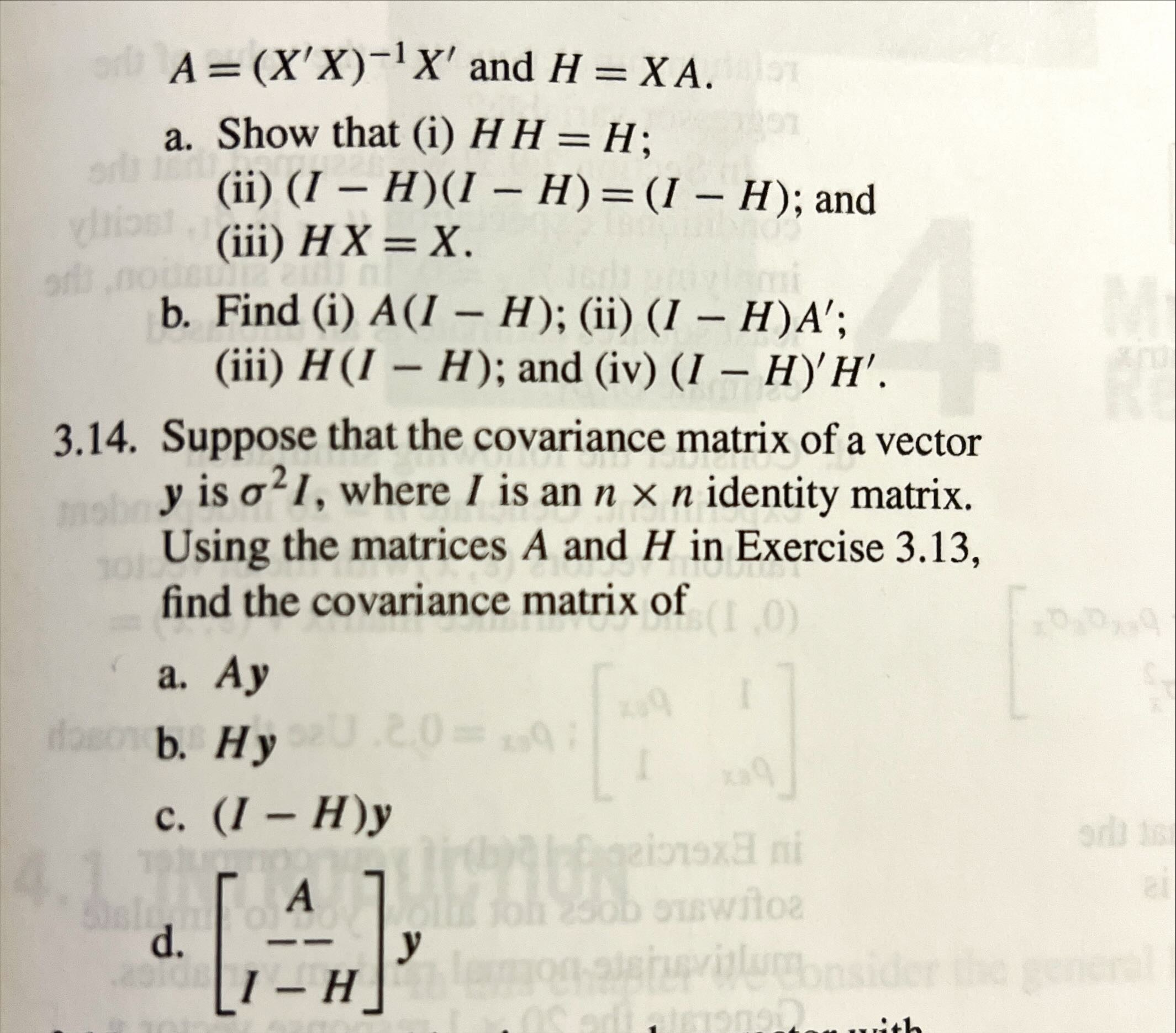
A = (X'X) -1 X' and H = XA. a. Show that (i) HH = H; (ii) (1 - H)(I - H) = (1 - H); and (iii) H X = X. of ,nous b. Find (i) A(1 - H); (ii) (1 - H)A'; (iii) H(1 - H); and (iv) (1 - H)'H'. 3.14. Suppose that the covariance matrix of a vector my is o'I, where I is an n x n identity matrix. Using the matrices A and H in Exercise 3.13, find the covariance matrix of (1 ,0) a. Ay doso b. Hy 62U .2.0 = 29 : c. (1 - H)y geionsx ni A ob ouswitor d. H mon