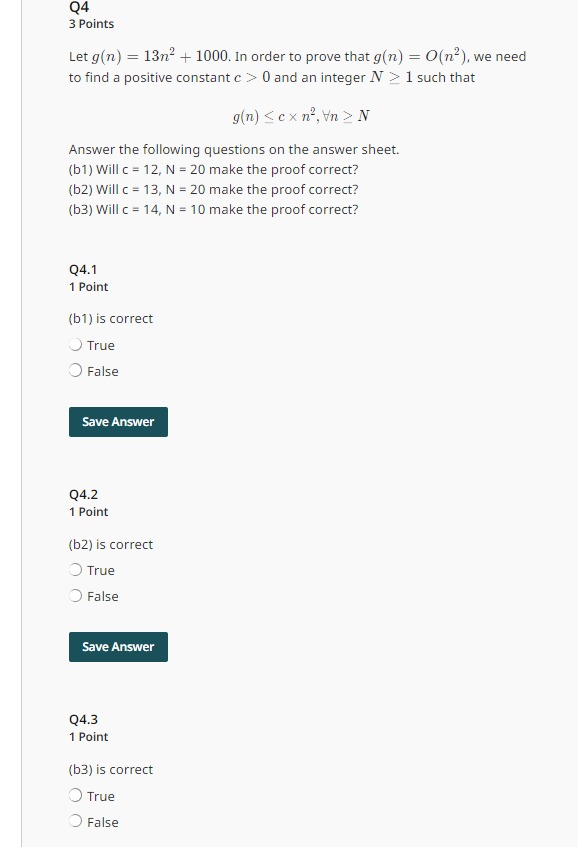
Q$4$

$3$ Points

Let $g(n)=13n^2+1000.$ In order to prove that $g(n)=O(n^2),$ we need

to find a positive constant $c>0$ and an integer $N1$ such that

$g(n)c{n}^2,$AAn$N$

Answer the following questions on the answer sheet.

$($b$1)$ Will c $=12,N=20$ make the proof correct?

$($b$2)$ Will $c=13,N=20$ make the proof correct?

$($b$3)$ Will $c=14,N=10$ make the proof correct?

Q$4\mathrm{.}1$

$1$ Point

$($b$1)$ is correct

True

False

Q$4\mathrm{.}2$

$1$ Point

$($b$2)$ is correct

True

False

Q$4\mathrm{.}3$

$1$ Point

$($b$3)$ is correct

True

False