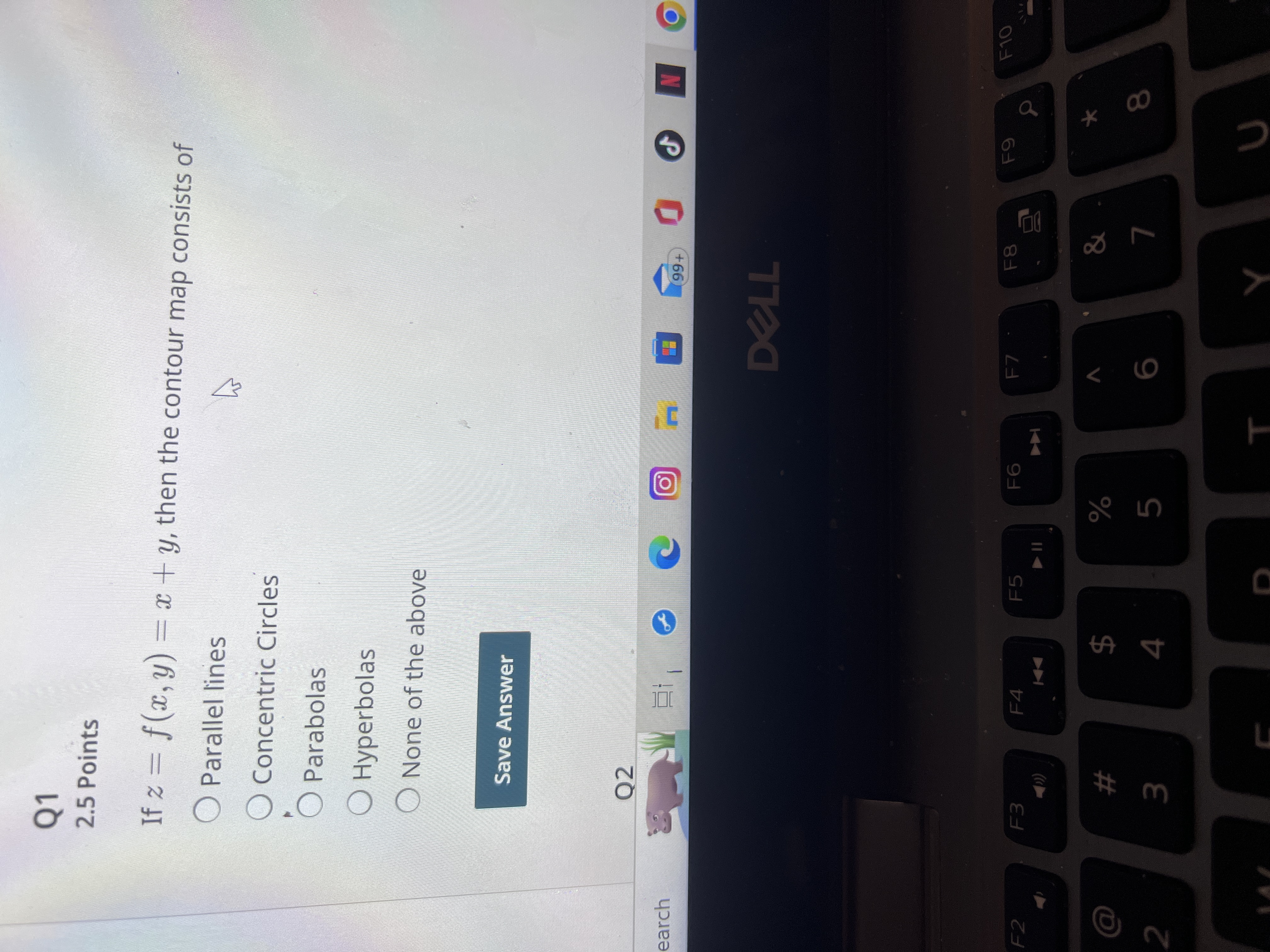
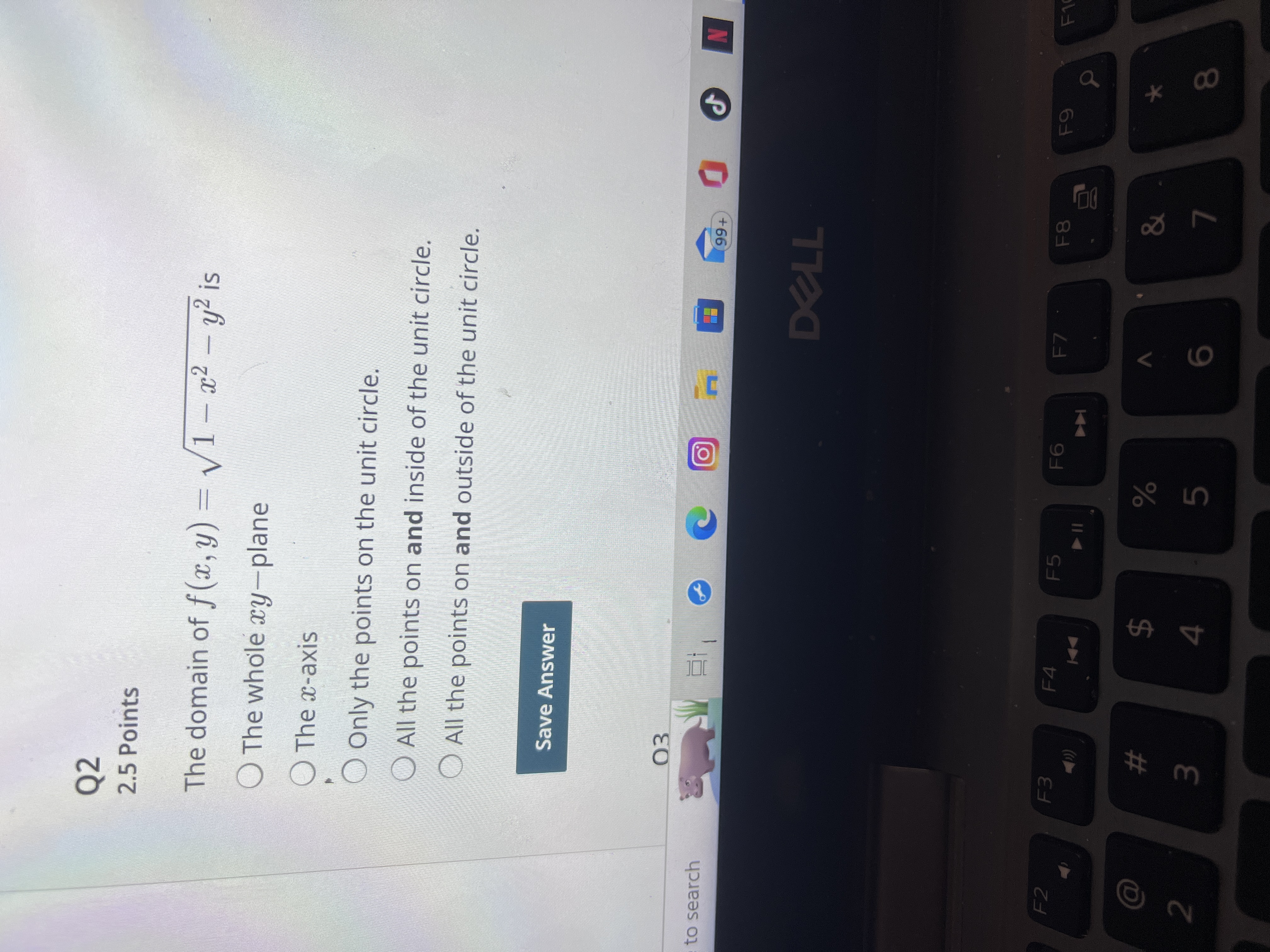
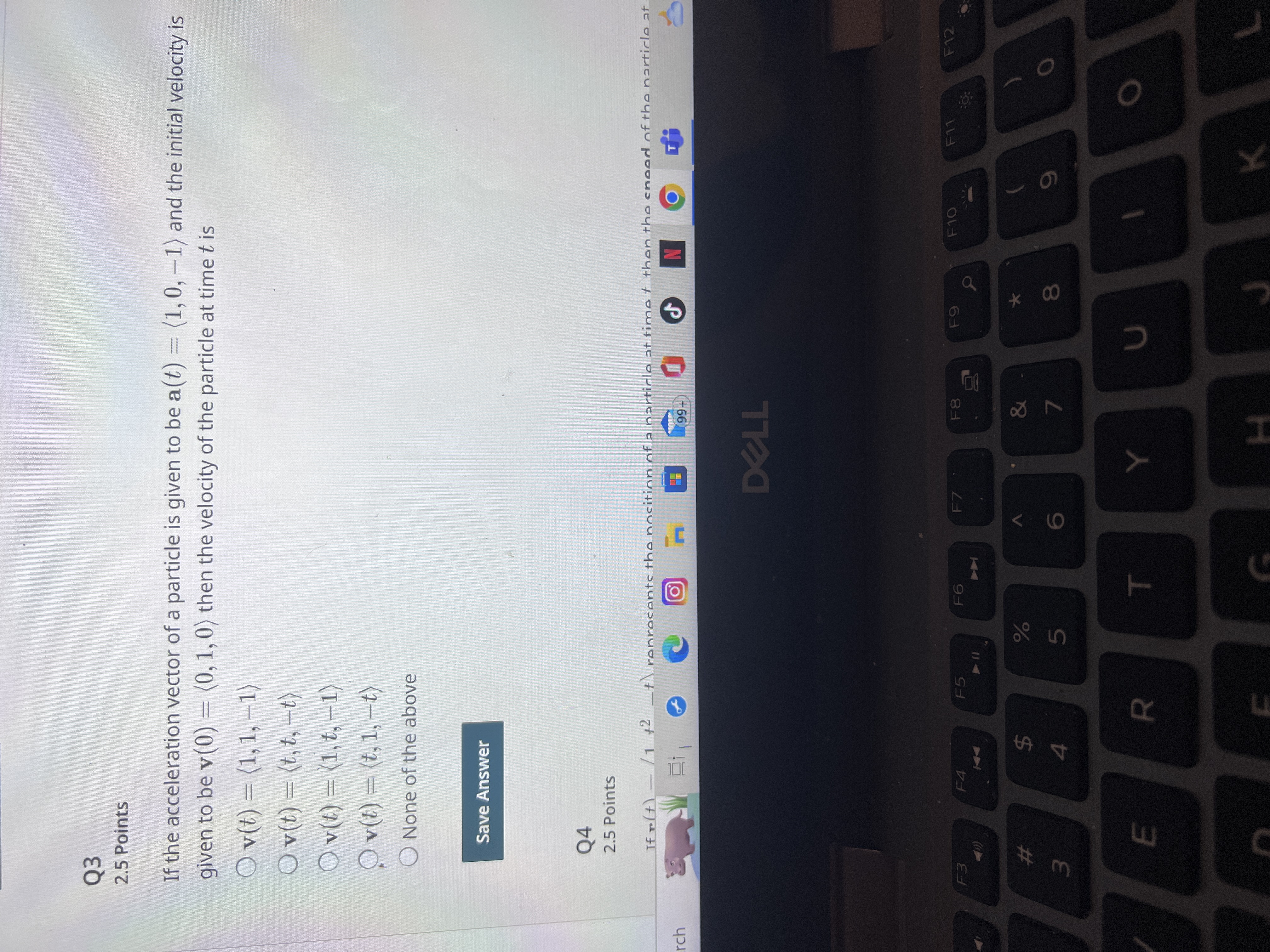
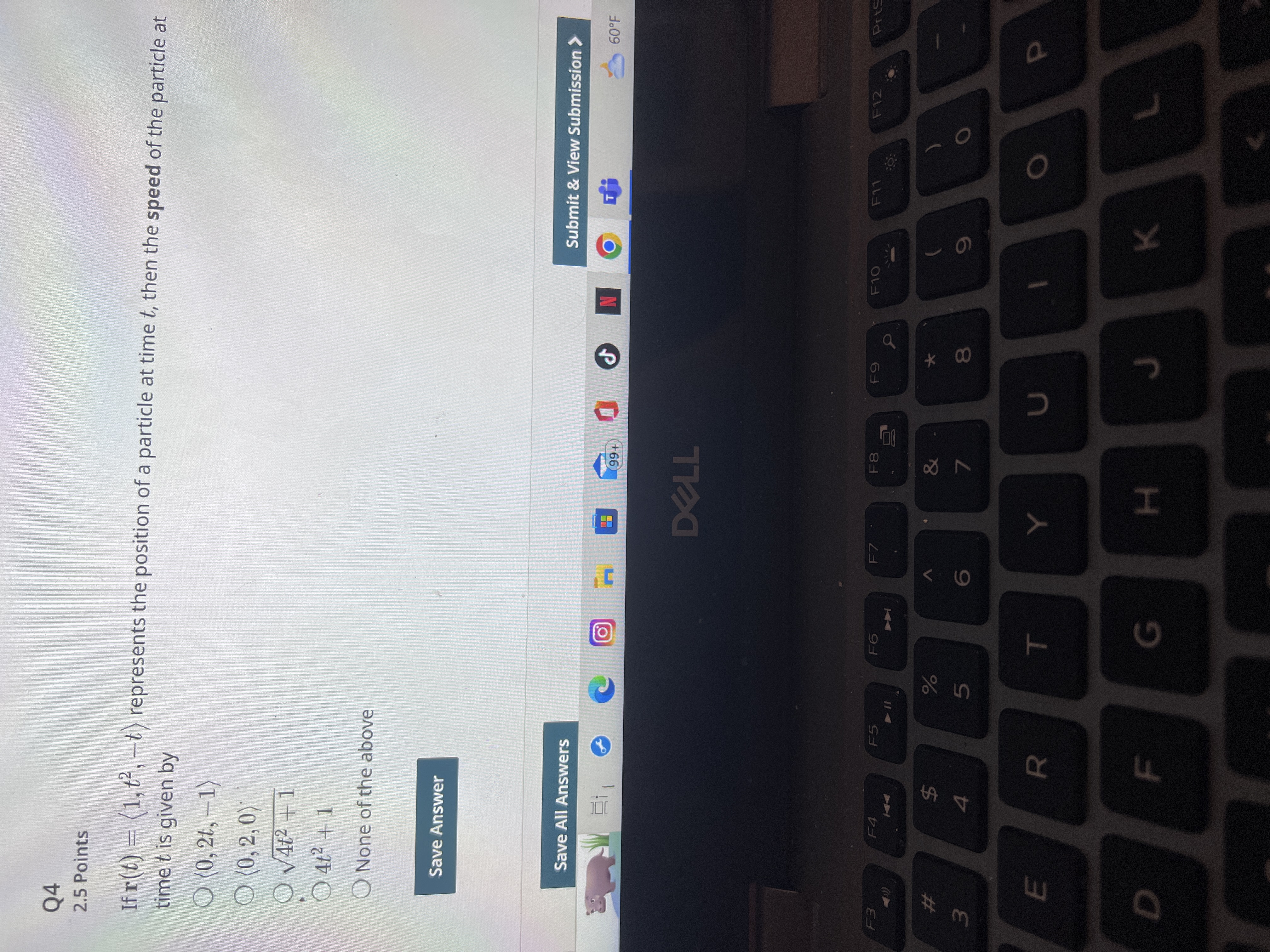
Q1 2.5 Points If z = f(x, y) = x + y, then the contour map consists of O Parallel lines O Concentric Circles O Parabolas Hyperbolas None of the above Save Answer earch Q2 F2 F3 2 # 3 F4 F5 $ SA 4 . 114 F6 14 n 0 N 99+ DELL F7 F8 F9 F10 % & 5 6 7 * 00 8 T U Q2 2.5 Points The domain of f(x, y) = 1 - x - y is O The whole xy-plane The x-axis Only the points on the unit circle. All the points on and inside of the unit circle. All the points on and outside of the unit circle. Save Answer to search 03 O 99+ DELL F2 F3 F4 F5 F6 F7 F8 2 # m 3 $ % olo in 4 5 00 0 F9 & 6 7 8 N F19 rch Q3 2.5 Points If the acceleration vector of a particle is given to be a(t) = (1, 0, -1) and the initial velocity is given to be v(0) = (0,1,0) then the velocity of the particle at time t is Ov(t) = (1,1,-1) Ov(t) = (t,t,t) v(t) = (1, t, 1) Ov(t) = (t, 1, t) None of the above F3 3 # Save Answer Q4 2.5 Points If r(+) - 1 +2 +\ enresents the nosition of a narticle at time t then the need of the narticle at O 99+ F4 DELL F5 F6 F7 F8 F9 F10 F11 F12 -0: % 5 dos $ 4 E R T L Y I 7 C 8* K Q4 2.5 Points If r(t) = (1, t, t) represents the position of a particle at time t, then the speed of the particle at time t is given by O (0,2t,-1) (0,2,0) 4t2 +1 4t+1 None of the above F3 #3 Save Answer Save All Answers O 99+ DELL N Submit & View Submission 60F F4 F5 F6 F7 F8 F9 F10 F11 F12 Pris $ #4 % dos 5 & 7 E R T Y U D F G H 8 * 9 J K O P