Question: Q1 . Consider the following linear programming problem and its optimal final tableau shown below. s.t. z x1 x2 x3 s1 s2 rhs 1 0
Q1. Consider the following linear programming problem and its optimal final tableau shown below.
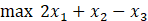
s.t. 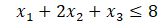
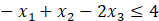
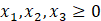
| z | x1 | x2 | x3 | s1 | s2 | rhs |
| 1 | 0 | 3 | 3 | 2 | 0 | 16 |
| 0 | 1 | 2 | 1 | 1 | 0 | 8 |
| 0 | 0 | 3 | -1 | 1 | 1 | 12 |
a.Write the dual problem and find the optimal dual variables from the above tableau.
b.Using sensitivity analysis, find the new optimal solution if the coefficient of 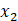 in the objective function is changed from 1 to 5.
in the objective function is changed from 1 to 5.
c.For what range of 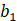 (the first constraint resource) will it remain feasible?
(the first constraint resource) will it remain feasible?
d.Suppose that a new activity 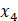 is proposed with unit return 4 and consumption vector
is proposed with unit return 4 and consumption vector 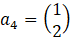 . Find the new optimal solution
. Find the new optimal solution
max2x1+x2x3 x1+2x2+x38 x1+x22x34 x1,x2,x30 x2 b1 x4 a4=(12)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


