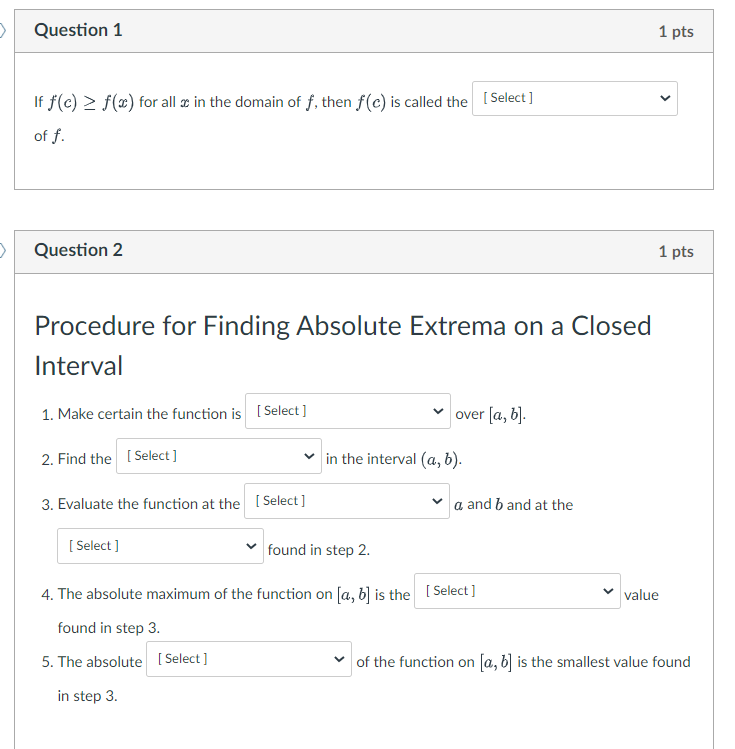
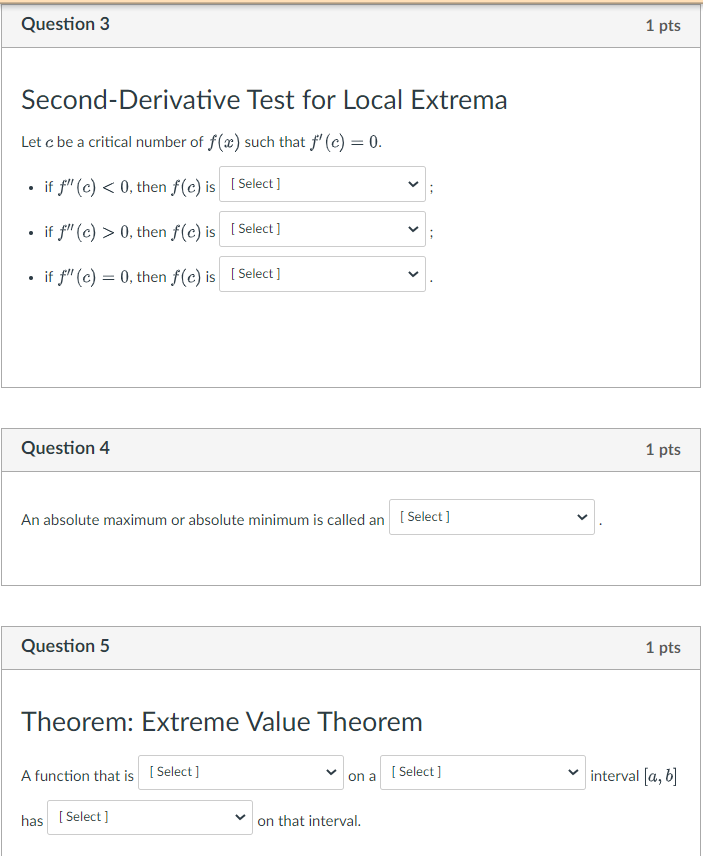
q1 dropdown options: absolute minimum, local minimum, absolute maximum, local maximum, inflection point

question 2:

1st dropdown options: continuous, linear, exponential, differentiable

2nd dropdown options: roots, inflection points, intercepts, critical numbers

3rd dropdown options for the first box: midpoints, endpoints, interior points 3rd dropdown options for the second box: inflection points, intercepts, critical numbers, roots

4th dropdown options: average, smallest, median, largest

5th dropdown options: minimum, maximum

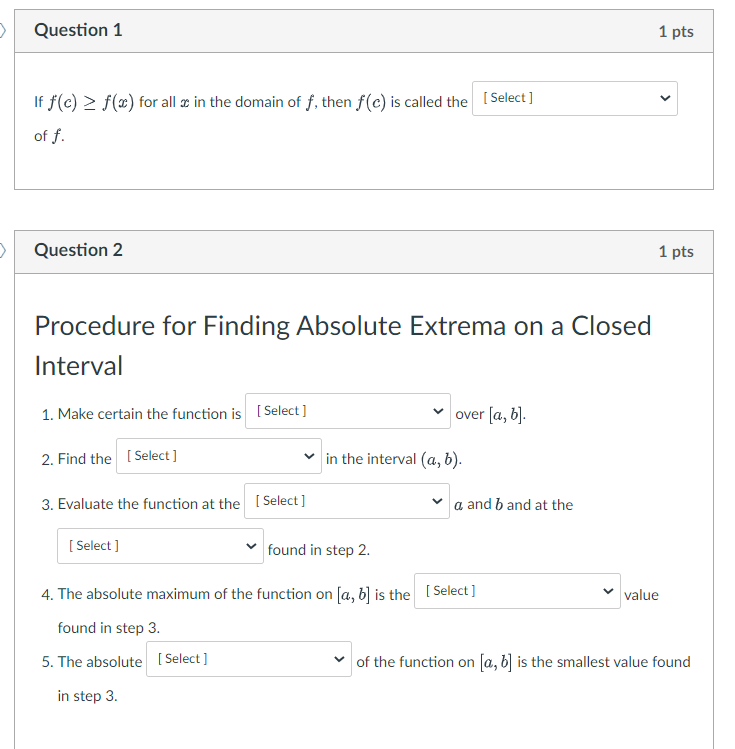
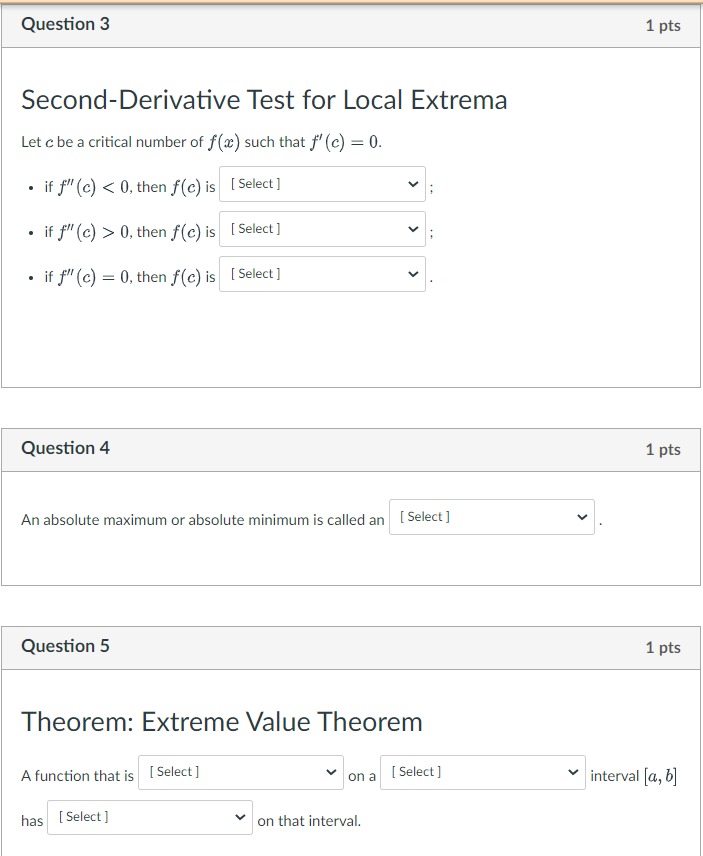
Question 1 1 pts If He) 2 x) for all 1: in the domain of f, then c] is called the [salad] V Question 2 1 pts Procedure for Finding Absolute Extrema on a Closed Interval 1. Make certain the function is [59'9\"] V over [a, b]. 2. Find the [Select] v in the interval (a, b). 3. Evaluate the function at the [59"9'3] V a and b and at the [59'9\"] V Found in step 2. 4. The absolute maximum of the Function on [a, b] is the [se'e] V value Found in step 3. S. The absolute [59'9'31] V oFthe function on [-51, b] is the smallest value found in step 3. Question 3 1 pts Second-Derivative Test for Local Extrema Let c be a critical number of f() such that f (c) = 0. . if f" (c) 0, then f(c) is [ Select ] . if f" (c) = 0, then f(c) is [ Select ] Question 4 1 pts An absolute maximum or absolute minimum is called an |[ Select ] Question 5 1 pts Theorem: Extreme Value Theorem A function that is [ Select ] on a [ Select ] interval [a, b] has [ Select ] on that interval