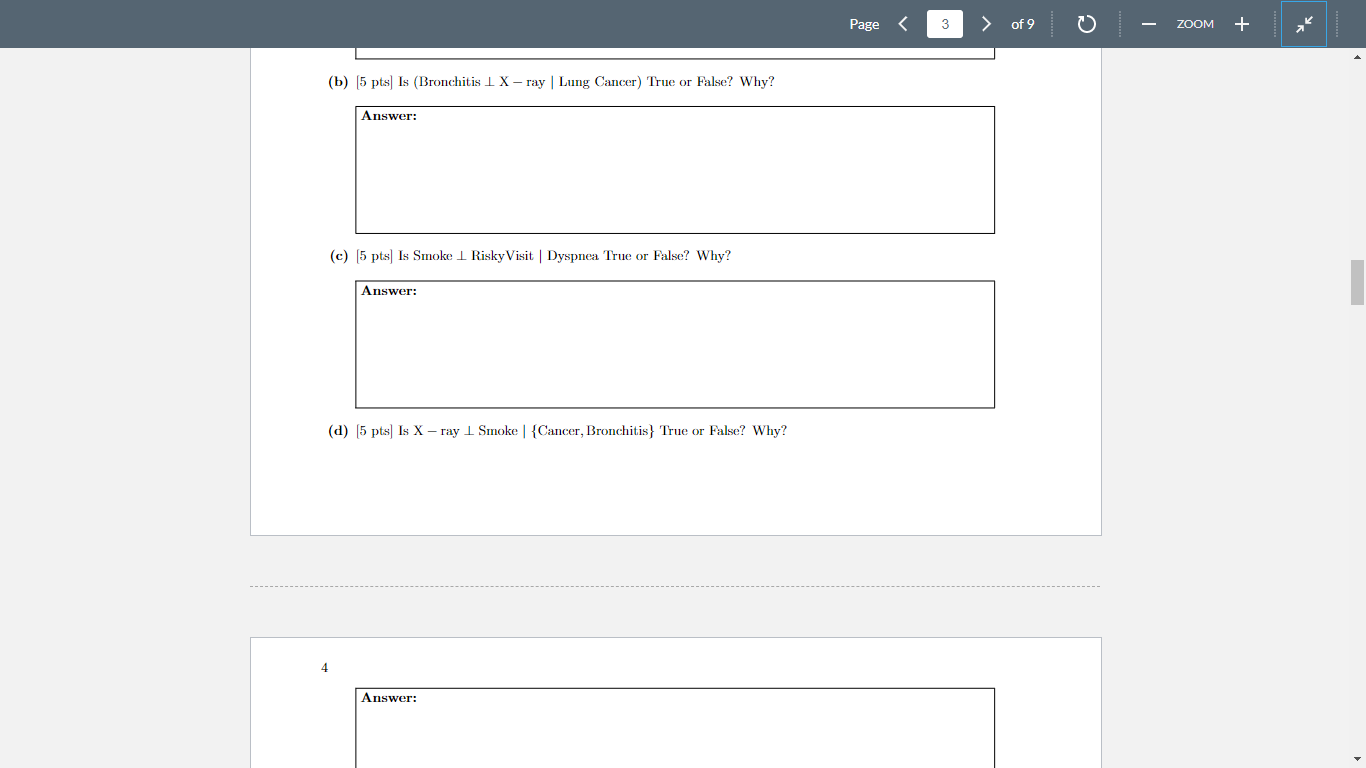
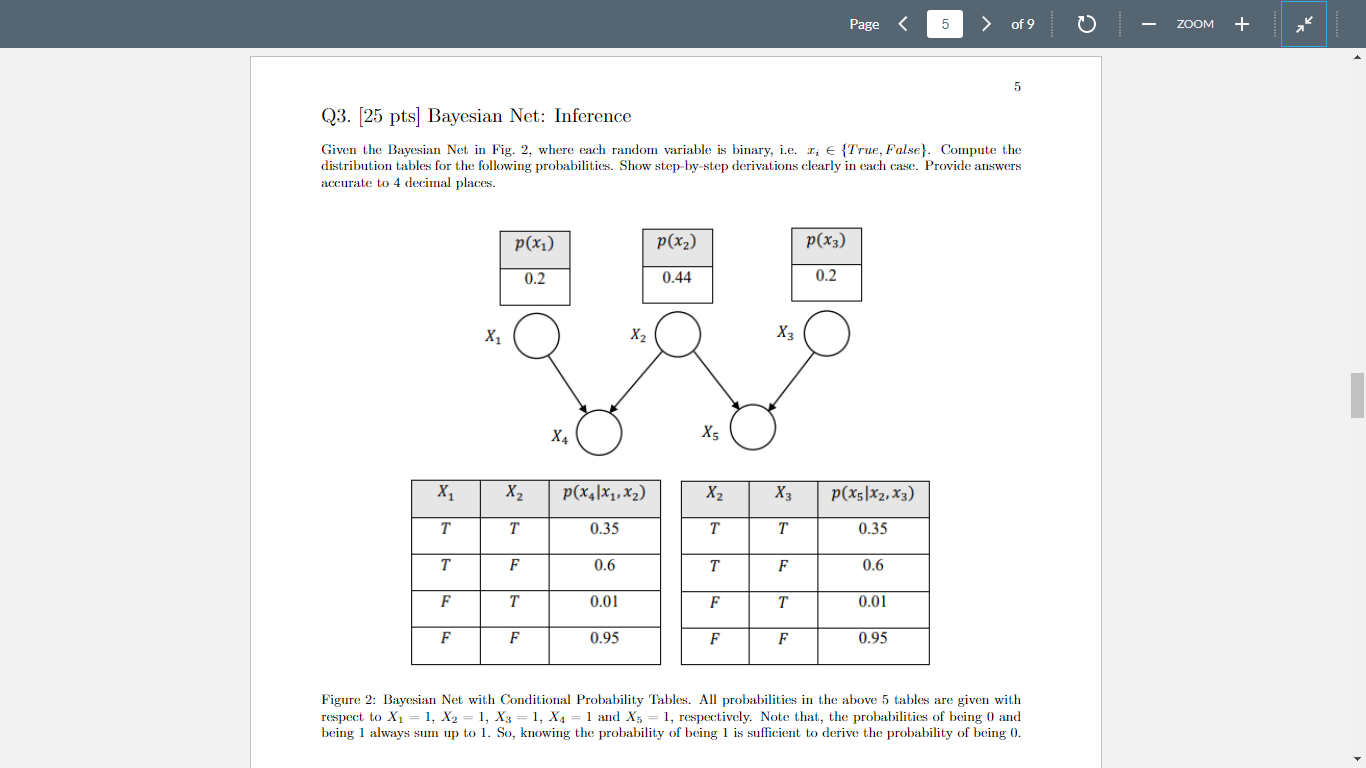
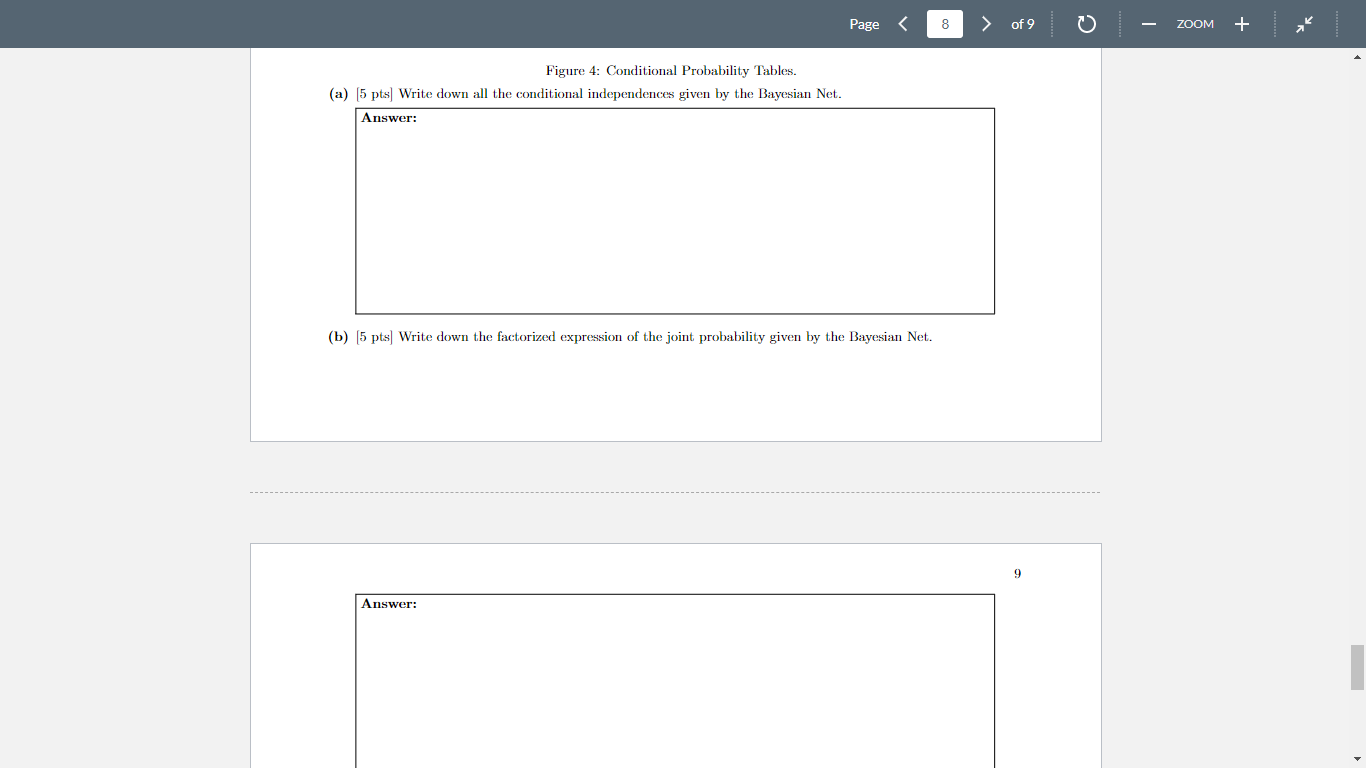
Q2. [20 pts] Bayesian Net: Conditional Independence Consider the Bayesian Net shown in Fig 1, which depicts the relationships among variables associated with chest abnormality. Answer the following questions based on the graphical model. Figure 1: Bayesian Net for Chest Abnormality. (a) [5 pts] Is (Smoke Dyspnea Bronchitis) True or False? Why? (b) [5 pts] Is (Bronchitis X - ray | Lung Cancer) True or False? Why? (b) [5 pts] Is (Bronchitis X - ray | Lung Cancer) True or False? Why? (c) [5 pts] Is Smoke RiskyVisit Dyspnea True or False? Why? (d) [5 pts ] Is X - ray Smoke | \{Cancer, Bronchitis\} True or False? Why? Q3. [25 pts] Bayesian Net: Inference Given the Bayesian Net in Fig. 2, where each random variable is binary, i.e. xi{ True, False }. Compute the distribution tables for the following probabilities. Show step-by-step derivations clearly in each case. Provide answers accurate to 4 decimal places. Figure 2: Bayesian Net with Conditional Probability Tables. All probabilities in the above 5 tables are given with respect to X1=1,X2=1,X3=1,X4=1 and X5=1, respectively. Note that, the probabilities of being 0 and being 1 always sum up to 1 . So, knowing the probability of being 1 is sufficient to derive the probability of being 0. (a) [5 pts ] (a) P(x1x5) (b) [5 ptss ] (b) P(x2x4) (e) [5pts] (d) P(x5) Q4. [25 pts] Bayesian Net: Inference Fig. 3 shows a Bayesian Net characterizing the causal relationship between 5 random variables x1,x2,x3,x4 and x5 where x1,x2,x4{0,1} while x3,x5{0,1,2}. Provide answers accurate to 4 decimal places. Figure 3: Bayesian Net. Figure 4: Conditional Probability Tables. 1 (b) [5 pts] Write down the factorized expression of the joint probability given by the Bayesian Net. (c) [15 pts ] Fig. 4 gives the probability tables of the Bayesian Net. Find the conditional probability table for p(x1x3=1,x2). Show step-by-step derivation clearly