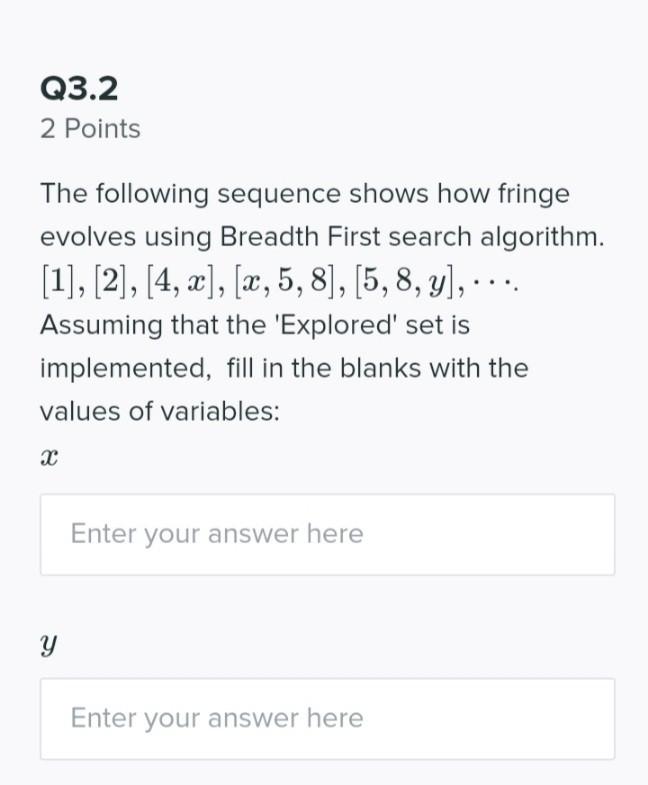
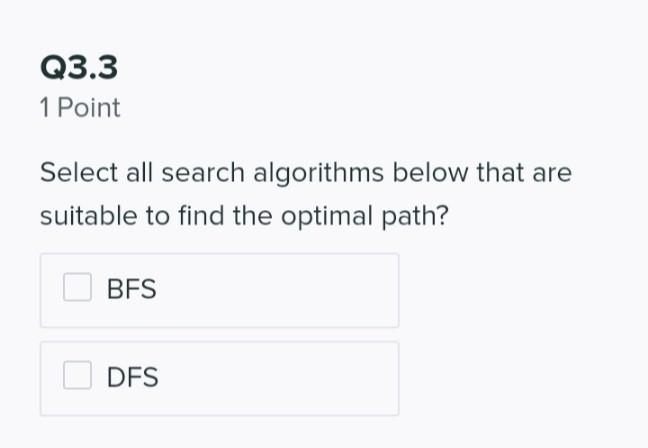
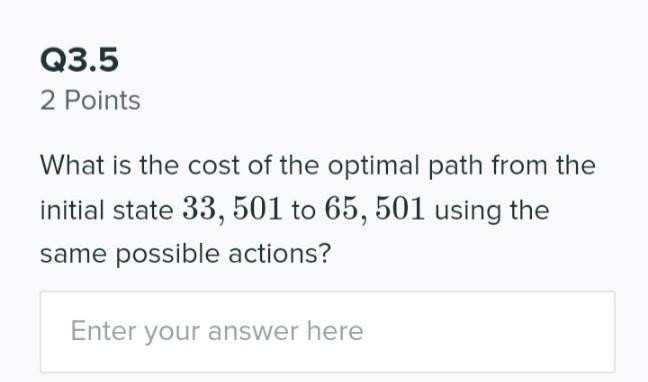
Q3 11 Points Consider a state-space where each state s is defined by a unique integer value, and the transitions between the states are possible only via two arithmetic actions on s: 1) adding 1, or II) multiplying by 2, resulting in the new states of s + 1 or 2s, respectively. Starting with the initial state of s = 1, the goal is to reach a certain goal state via an optimal path involving the least number of the actions above. Q3.1 2 Points The following sequence shows how fringe evolves using Depth First search algorithm. [1], [2], [4, x], [8, y, x], Fill in the blanks with the values of variables: Enter your answer here y Q3.2 2 Points The following sequence shows how fringe evolves using Breadth First search algorithm. [1], [2], [4, 2], [x, 5, 8], [5, 8, y),... Assuming that the 'Explored' set is implemented, fill in the blanks with the values of variables: Enter your answer here Enter your answer here Q3.3 1 Point Select all search algorithms below that are suitable to find the optimal path? BFS DFS Q3.4 4 Points Assume that the states are defined using binary representation. For example, 5 1 x 22 + 0 x 21 +1 2 = (101)2. This binary code can be obtained using the following course of arithmetic actions: 1 + 10 + 100 + 101. Generalising the X 2 given example, what is the cost of the optimal path from the initial state 1 to 65,501 only using the actions above? X2 +1 Enter your answer here Q3.5 2 Points What is the cost of the optimal path from the initial state 33, 501 to 65, 501 using the same possible actions? Enter your answer here Q3 11 Points Consider a state-space where each state s is defined by a unique integer value, and the transitions between the states are possible only via two arithmetic actions on s: 1) adding 1, or II) multiplying by 2, resulting in the new states of s + 1 or 2s, respectively. Starting with the initial state of s = 1, the goal is to reach a certain goal state via an optimal path involving the least number of the actions above. Q3.1 2 Points The following sequence shows how fringe evolves using Depth First search algorithm. [1], [2], [4, x], [8, y, x], Fill in the blanks with the values of variables: Enter your answer here y Q3.2 2 Points The following sequence shows how fringe evolves using Breadth First search algorithm. [1], [2], [4, 2], [x, 5, 8], [5, 8, y),... Assuming that the 'Explored' set is implemented, fill in the blanks with the values of variables: Enter your answer here Enter your answer here Q3.3 1 Point Select all search algorithms below that are suitable to find the optimal path? BFS DFS Q3.4 4 Points Assume that the states are defined using binary representation. For example, 5 1 x 22 + 0 x 21 +1 2 = (101)2. This binary code can be obtained using the following course of arithmetic actions: 1 + 10 + 100 + 101. Generalising the X 2 given example, what is the cost of the optimal path from the initial state 1 to 65,501 only using the actions above? X2 +1 Enter your answer here Q3.5 2 Points What is the cost of the optimal path from the initial state 33, 501 to 65, 501 using the same possible actions? Enter your answer here