Question: Q3: Consider the function defined on the whole zyplane: [F it (z,y) (0,0) f(?:, y) { +u f (I: y) - {{L ) (a) Using

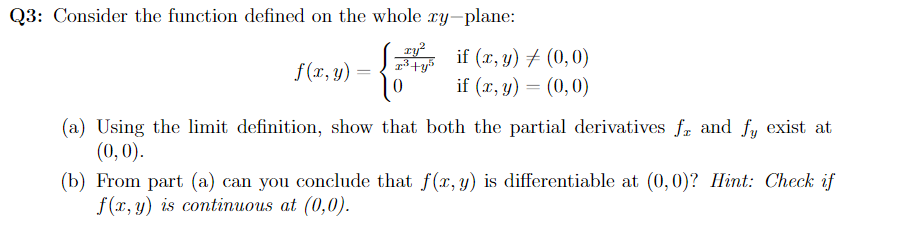
Q3: Consider the function defined on the whole zyplane: [F it (z,y) (0,0) f(?:, y) { +u f (I: y) - {{L ) (a) Using the limit definition, show that both the partial derivatives f, and f, exist at (0,0). (b) From part (a) can you conclude that f(z,y) is differentiable at (0,0)? Hint: Check if f(z,y) is continuous at (0,0)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1 Multivariable functions and vector geometry Due date and time: Wednesday, June 7th at 9:30 AM in lecture Please ensure that you have read and understood the document \"Homework Guidelines" on the...

- Question 1 Which of the following statements is the Extreme Value Theorem? If f attains a local maximum and a local minimum on an interval [a, b), then f is continuous. If f is a continuous...

Kindly give only correct answers showing your steps 1. (a) Use the Intermediate Value Theorem to show that the equation - sin (x) + sin(x) =-1 has at least two distinct real solutions on (0, ce)....

answer all For a floating-point implementation with p = 4, = 10, explain the round to even method of rounding using the half-way cases 7.3125, 7.3175 as examples. To illustrate how their modes of...

Economics question 3. Consider the function f(x, y) = (2 - }) defined on {(x, y) : 1, y > 0}. (a) Graph {(r, y) : x, y > 0, f(x, y) = -1}. (b) Find an equation of the hyperplane tangent to the graph...

Suggest two logical formulae that might appear in Evil Robot's knowledge base in order to describe the initial state for the above problem ------MOREOVER DETAILS --------- Specification and...

ecoty 1. Suppose that a consumer with utility U(x1, 12) is given an initial endowment 71, 12 so that his total budget set is pill , p232 (a) Derive a formula for the slutsky equation with endowments...

ot . Consider the function defined by f(z) =In(y/|1 z2|). e (1 mark) State the domain of this function. (2 marks) Determine the derivative of In(,/|1 z2|). Be careful to show all your work. . (3...

What can we conclude about the functional dependency AsZ sAW? Explain your answer. [4 marks] (c) In the process of using functional dependencies to normalise a schema, what is meant by a lossless...

WAMAP * f Facebook x | + O X - C wamap.org/assess2/?cid=27419&aid=1403877#/full t 2hrs16mins X . Question 6 5 pts 9 5 0 Details A cable will be installed from a farmhouse to a series of telephone...

Gadget Co invests in a $100,000 bond with an 8% coupon rate. The market rate of interest is 10% annually and it is a 5 year bond 1. Assuming the company invests on January 1st and only pays $92,418...

We can use bond-line formulas to represent alkenes in much the same way that we use them to represent alkanes. Consider the following alkene: (a) What is its IUPAC name? (b) How many carbon atoms are...

The use of advanced technology and data analytics is increasingly standard practice among audit firms. These tools enhance auditors' ability to organize data and support more informed, timely...

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...