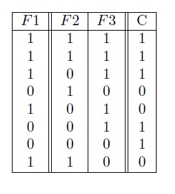
Question: Q4. Consider the following data in the attribute-instance format. Perform feature selection using Sequential Forward Selection (SFS) with consistency rate as the subset evaluation metric,
Q4. Consider the following data in the attribute-instance format. Perform feature selection using Sequential Forward Selection (SFS) with consistency rate as the subset evaluation metric, stopping after two features have been selected.
Q5. Suppose the following are all of the frequent patterns mined from certain dataset:
B:3,C:2,D:3,E:3,M:2,N:2,BD:3,CD:2,DE:3,EM:2,EN:2,MN:2, EMN:2
Find all frequent closed itemsets together with their supports; using the frequent patterns.
Q6. Based on the frequent patterns given above, give all association rules (including their support and confidence) having E as their left-hand side. Type right-arrow as ->
Q7. Consider the following dataset D with four transactions, and assume minSupp=50% and minConf=80%. Find all frequent patterns from D using the Apriori algorithm (using alphabetic order for item ordering). You need to give enough details, including showing the join-prune steps of the algorithm.
| TID | Transactions |
| T1 | {M,O,K,E,Y} |
| T2 | {D,O,K,E,Y} |
| T3 | {M,A,K,E} |
| T4 | {M,U,K,Y} |
Q8. Draw a hash tree for the following set of 3-itemsets (as candidate 3-itemsets): ACD,CDE, CEI,CIM,CNO.
Use h(A)=0, h(C) = 1, h(D) = 2, h(E)=0, h(I)=1, h(K)=2, h(M)=0, h(N)=1, h(O)=2, h(U)=0, h(Y)=1.
Assume each non-leaf-level node can hold up to three itemsets. A left-level node is a node that cannot be split in the hash tree even when it is full.
\begin{tabular}{|c||c|c||c|} \hlineF1 & F2 & F3 & C \\ \hline 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \\ \hline \end{tabular}
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


